Introduction
To improve generalization in reinforcement learning, modern methods often resort to 1) regularization techniques in deep learning, such as data augmentation, batch normalization and etc, and 2) representation learning.
In this post, we discuss Invariant Decoupled Advantage Actor-Critic(IDAAC), proposed by Raileanu&Fergus 2021, which identifies the problem of using a shared representation for learning the value function and the policy, and addresses it by decoupling the policy and value function. To ensure a good representation for policy learning, IDAAC further augments the policy loss with an advantage prediction loss and an auxiliary loss.
Note that the paper is incomplete at the time of writing this post, there are still some details incorrect and missing. However, the problem it identifies is noteworthy.
Problem of a Shared Representation for The Value Function and The Policy
Value function often requires instance-specific features in addition to the information needed to determine the optimal policy. Instance-specific features often carry information specific to the training environment instance, such as the background color, that helps memorize what the future will be or how far we are from the goal. These features are usually important to the value function as they help to produce more accurate prediction. On the other hand, they could be detrimental to the policy learning as they are irrelevant to the decision making process(not if the ). Worse still, instance-specific information at the test time is usually different from that at the training time. Therefore, incorporating instance-specific information in policy learning can easily lead to a policy that overfits the training environments.
Methods
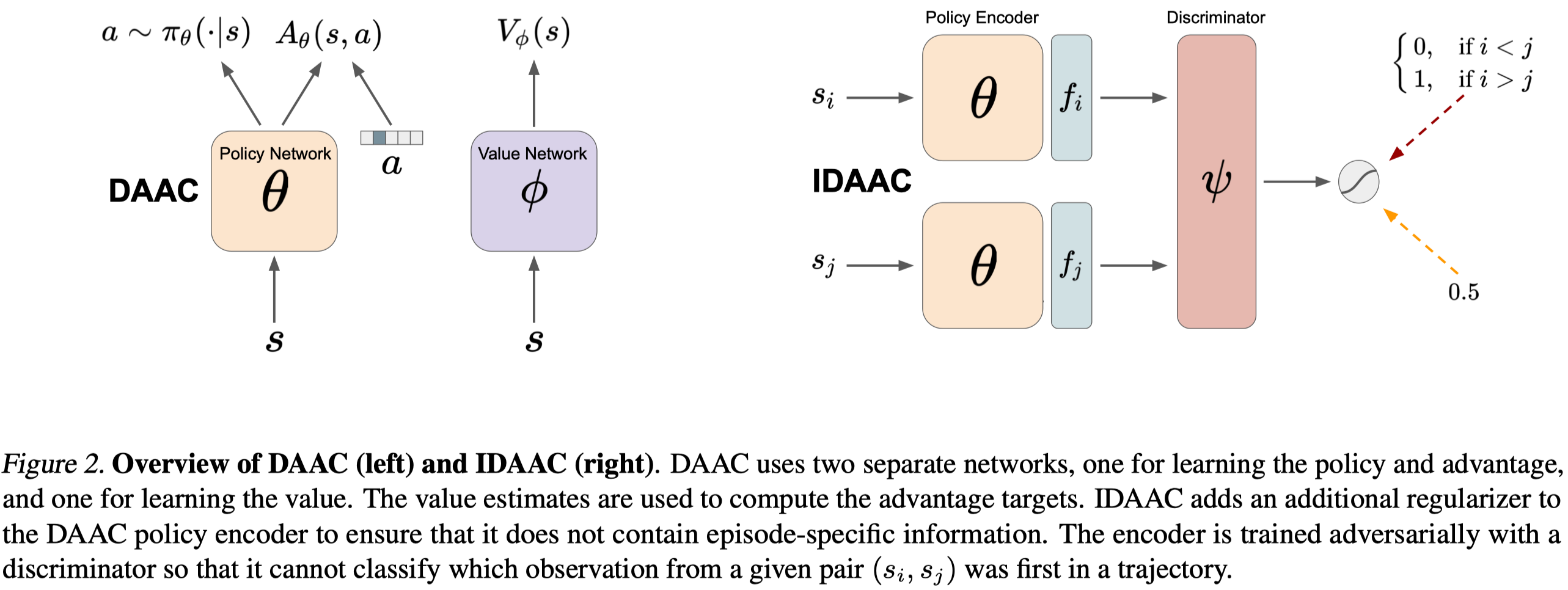
In this section, we first introduce Decoupled Advantage Actor-Critic(DAAC) that decouples the policy and the value functions and augment the policy loss with an advantage prediction loss. Then we discuss Invariant Decoupled Advantage Actor-Critic(IDAAC) that further augments the policy loss with an auxiliary loss.
Decoupled Advantage Actor-Critic
DAAC use separate networks for the policy and the value function. The value function is the same as the one in PPG, with the usual value prediction loss. The policy network is trained to maximizes the following objective
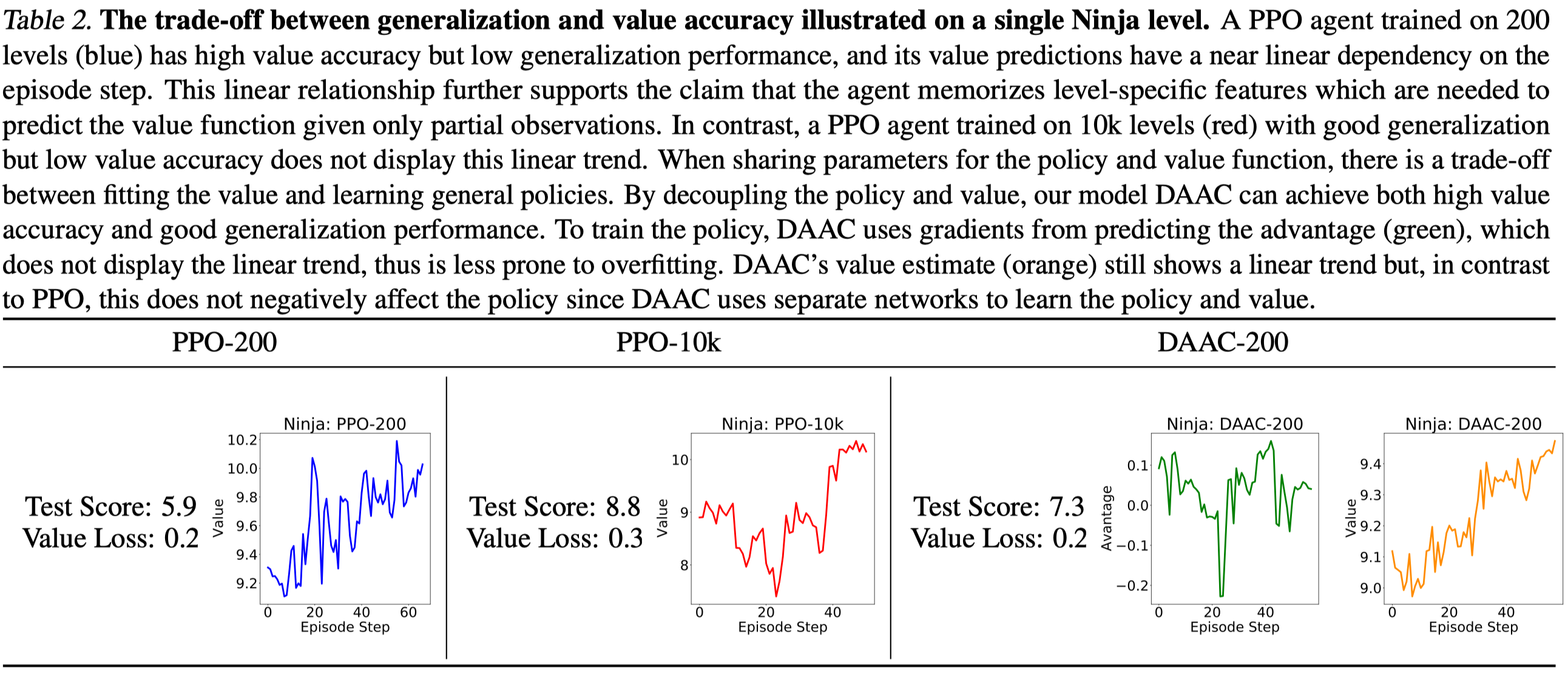
\[\begin{align} \mathcal J_{DAAC}=\mathcal J(\pi_\theta) + \alpha_e\mathcal H(\pi_\theta)-\alpha_a\mathcal L_A(\theta) \end{align}\]where \(\mathcal J(\pi_\theta)\) is the PPO objective, \(\mathcal H(\pi_\theta)\) is the entropy term, and \(\mathcal L_A(\theta)\) is the advantage loss for the advantage stream, which shares the representation with the policy. The advantage loss is used here because experiments(Table 2) show that the advantage is less prone to overfit the idiosyncrasies of an environment. Intuitively, because the advantage is a relative measure of an action’s value while the value is an absolute measure of a state’s value, the advantage does not vary as much with the number of remaining steps and thus less likely to overfit to instance-specific information.
Invariant Decoupled Advantage Actor-Critic
To further encourage the policy to learn a representation that’s invariant to the time step. IDAAC introduces an adversarial network in which the discriminator \(D_\psi\) learns to distinguish which observation from a given pair came first within an episode and the encoder \(E_\theta\), which share the same parameter with the policy network, learns to generate a representation that can fool the discriminator.
We train the discriminator using a cross-entropy loss
\[\begin{align} \mathcal L(D_\psi)=-\log D_\psi(E_\theta(x^\tau_i), E_\theta(x^\tau_j))-\log(1-D_\psi(E_\theta(x_i^\tau,x_j^{\tau'}))) \end{align}\]where \(\tau\) and \(\tau’\) represent two different trajectories, and \(i<j\) denote the time step—the ordering only matters when the discriminator is able to interpret sequential data(for example, with an RNN). If the discriminator is a feed forward network, the ordering does not establish any difference and the discriminator only learns to distinguish if two observations are from the same trajectory. Unfortunately, the paper is still under review and does not present any details about the discriminator network for now.
The encoder \(E_\theta\) maximizes the uncertainty (entropy) of the discriminator
\[\begin{align} \mathcal J(E_\theta)={1\over 2}\log D_\psi(E_\theta(s_i), E_\theta(s_j))+{1\over 2}\log (1-D_\psi(E_\theta(s_i), E_\theta(s_j))) \end{align}\]The final policy objective is
\[\begin{align} \mathcal J_{DAAC}=\mathcal J(\pi_\theta) + \alpha_e\mathcal H(\pi_\theta)-\alpha_a\mathcal L_A(\theta)+\alpha_i\mathcal J(E_\theta) \end{align}\]Training Process
DAAC and IDAAC trains in the similar way as PPO except that for each iteration, it performs 1 policy epoch and 9 value epochs. Note that this makes the comparison with PPO and PPG unfair.
Experimental Results
We briefly summarize experimental results below. Note that the comparison may be biased since DAAC and IDAAC use a different training process than PPO and PPG(BTW, they do not disclose the training details of PPG!)
- Both methods exhibit SOTA generalization performance on the Procgen suite
- DAAC performs better than PPO with an additional advantage head and DVAC(DVAC is an ablation of DAAC that learns to predict the value rather than the advantage for the network). This shows that value prediction indeed impairs the policy. However, there are two subtleties needed to be aware. First, DAAC and PPO adopt different training paradigms. Second, DVAC uses unnormalized value prediction while DAAC use normalized advantage prediction; it’s unclear what a role normalization plays in these experiments.
- Training with more environment levels increases the generalization as well as the value loss. This is something expected as it becomes more challenging for the value function to predict as the data volume grows.
Discussions
Does Advantage Use Less Instance-Specific Features?
Thought Table 2 shows the advantage estimate does not exhibit a linear trend, but is it due to the advantage normalization? Raileanu&Fergus 2021 indeed experiments with PPO with normalized returns, finding it in general hurts the performance. However, the detail of PPO with normalized returns is missing. The experiment will be pointless if there is no additional separate value network trained to approximate unnormalized returns.
References
Raileanu, Roberta, and Rob Fergus. 2021. “Decoupling Value and Policy for Generalization in Reinforcement Learning.” http://arxiv.org/abs/2102.10330.

