Introduction
We present some hypotheses and experimental results on DQN conducted by Hasselt et al. 2018.
Hypotheses
Hypothesis 1 (Deep divergence) Unbounded divergence is uncommon when combining Q-learning and conventional deep reinforcement learning function spaces.
Hypothesis 2 (Target networks) There is less divergence when bootstrapping on separate networks.
Hypothesis 3 (Overestimation) There is less divergence when correcting for overestimation bias.
Hypothesis 4 (Multi-step) Longer multi-step returns will diverge less easily.
Hypothesis 5 (Capacity) Larger, more flexible networks will diverge less easily.
Hypothesis 6 (prioritization) Stronger prioritization of updates will diverge more easily.
Metrics
As we concerns whether the \(Q\) value will diverge we study the maximum absolute action value estimate, denoted “maximal \(\vert Q\vert \)”. We use this statistic to measure stability of the value estimates. Because the rewards are clipped to \([−1, 1]\), and because the discount factor \(\gamma\) is \(0.99\), the maximum absolute true value in each game is bounded by \({1\over 1-\gamma}=100\) (and realistically attainable values are typically much smaller). Therefore, values for which \(\vert q\vert > 100\) are unrealistic. We call this phenomenon soft divergence.
van Hasselt et al. 2018 conduct a large scale study on all 57 Atari games, with 336 parameter settings for DQN. Therefore, the following experimental results are relatively strong and general
Experimental Results
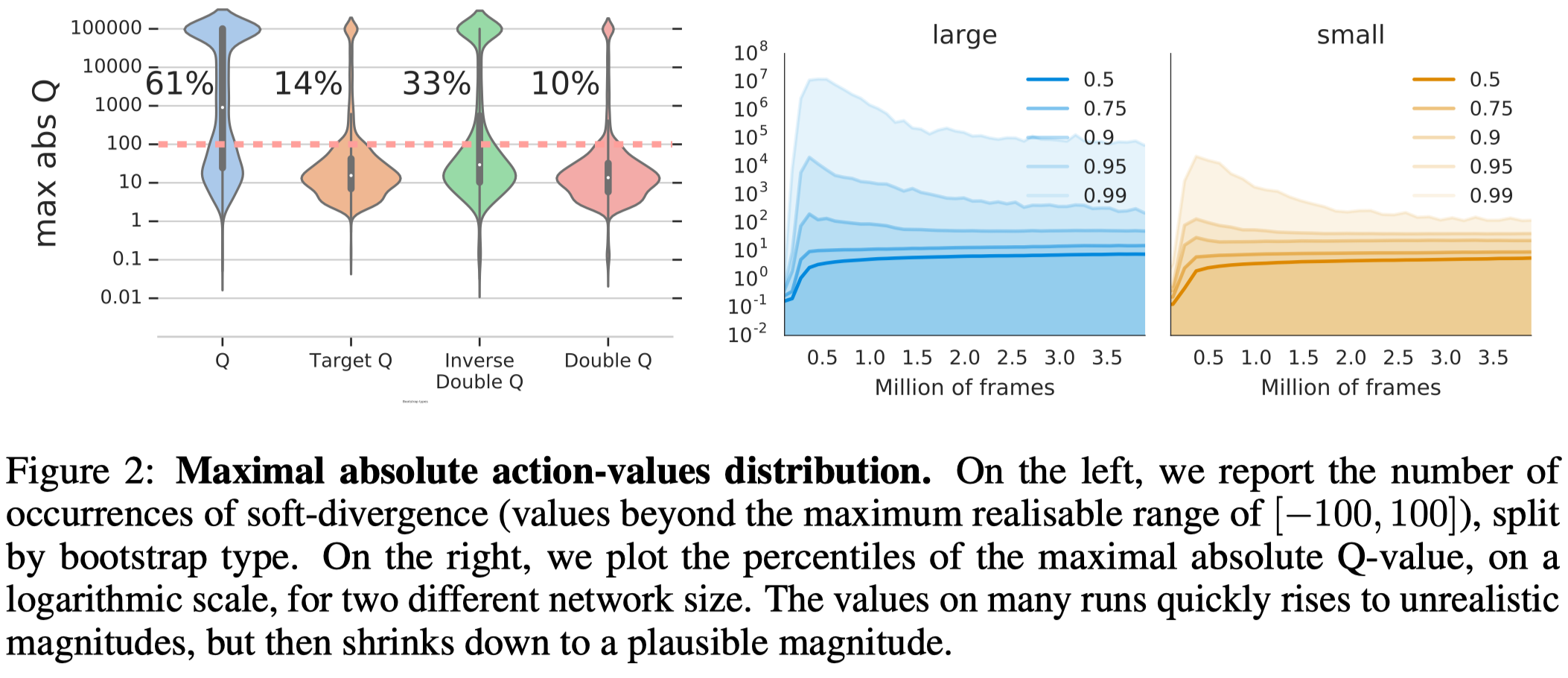
Figure 2 shows that soft divergence does occur, but they never became unbounded(producing floating point NaNs). This supports Hypothesis 1 that unbounded divergence rarely occurs in deep Q-learning.
The leftmost plot of Figure 2 shows that the target network and double DQN can effectively reduce the soft divergence (Hypothesis 2 an 3).
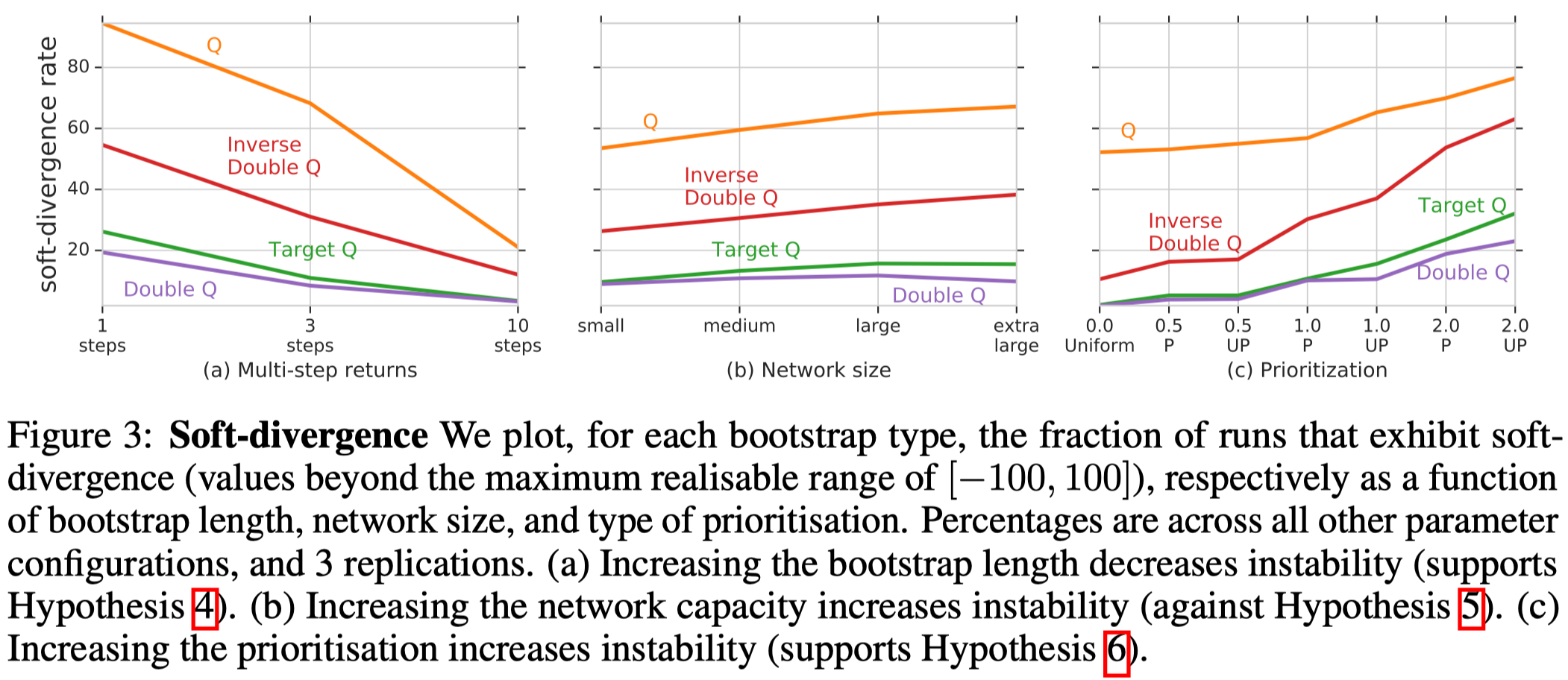
Figure 3a shows that longer multi-step returns greatly reduce the soft-divergence (Hypothesis 4).
Figure 3b runs counter to Hypothesis 5, showing that large network may increase the divergence. But as we will see latter, a larger network usually yields better performance.
Figure 3c shows strong prioritization can lead to instability (Hypothesis 6).
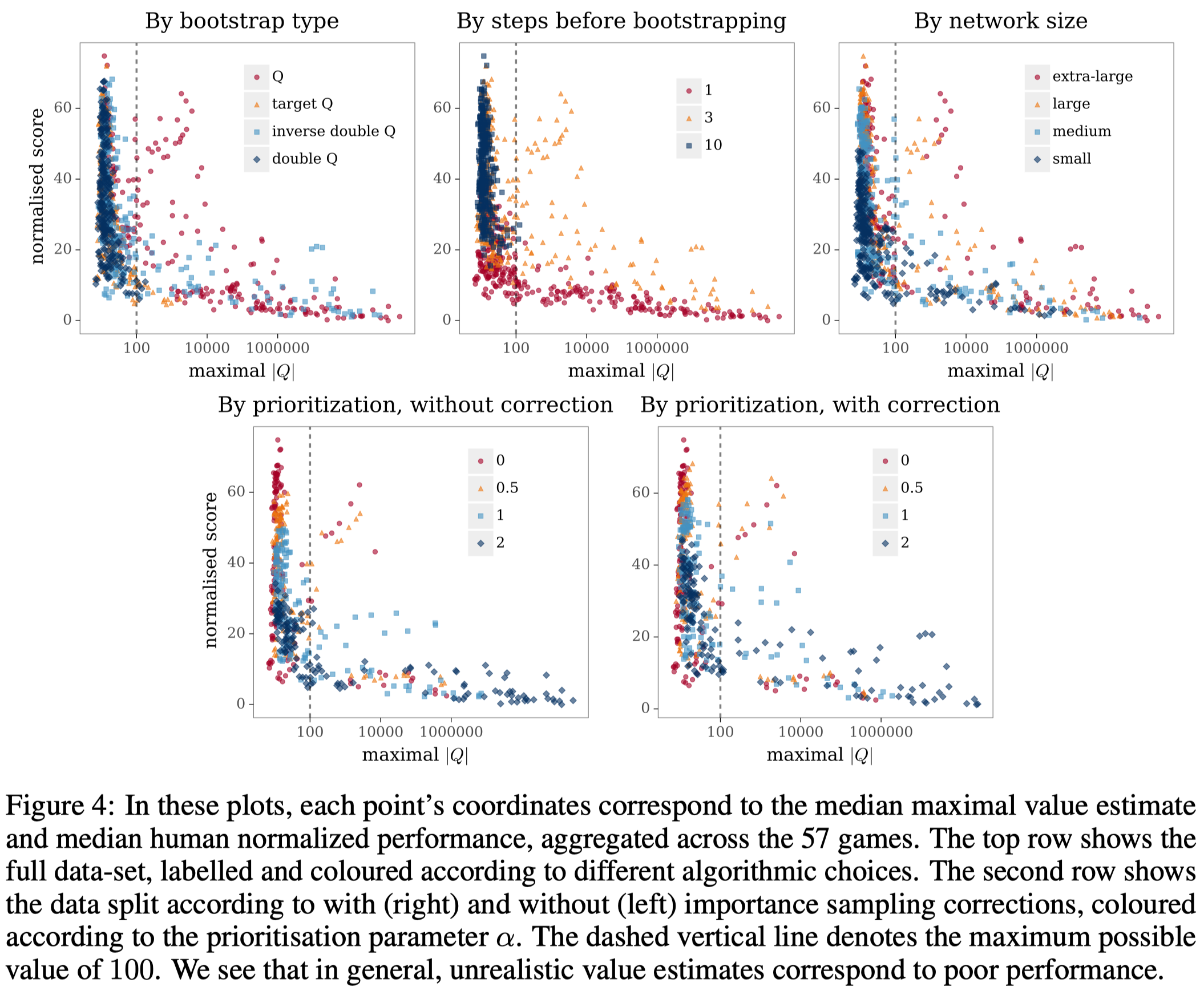
The top-left plot and the top-center plot of Figure 4 show that soft divergence caused by overestimation bias and short bootstrap length often leads to worse performance.
A different pattern emerges in network capacity. In the top-right plot of Figure 4, although large networks are more likely to increase the divergence, they yield better performance. One hypothesis is that when the network is large, the update of the value function may not be generalized to next state, which helps stabilize the target value,
The two plots in the bottom row of Figure 4 shows that large prioritization correlates both with divergence and reduced performance. It also shows correction in prioritized experience replay helps, but only to a small extent.
References
van Hasselt, Hado, Florian Strub, Joseph Modayil, Matteo Hessel, and Nicolas Sonnerat. 2018. “Deep Reinforcement Learning and the Deadly Triad.”

