Introduction
Like other deep learning domains, deep reinforcemeng learning agents are subject to overfitting. Often simple changes to the background could results in failure of a well-trained agent. Recently, there have been many research works trying to improve the generalization ability of RL agent by applying domain randomization/data augmentation to the observations. We discuss the work of Lee et al., which proposes distorting the observations using a random network. Like data augmentation methods, this encourages the agent to learn invariant and robust representations, whereby improving the generalization performance.
Network Randomization
Lee et al. trains an agent using a randomized input \(\hat o=f(o;\phi)\), where \(\phi\) is the parameter of the random network(typically, a single convolutional layer) and is reinitialized periodically. This provides varied and randomized input observations and motivates the agent to learn invariant representations.
To impose invariance to the random perturbation, the following feature matching loss is applied
\[\begin{align} \mathcal L_{FM}=\mathbb E[\Vert h(f(o;\phi);\theta)-sg(h(o;\theta))\Vert^2] \end{align}\]where \(h(\cdot)\) denotes the output of the penultimate layer of the network and \(sg\) is the stop_gradient operation. This loss draws features from randomized input close to features from original input. The total loss now becomes
where \(\beta\) is a hyperparameter(\(0.002\) used in the paper).
Random Network Initialization
To avoid complicating training, \(\phi\) is initialized using a mixture of identity and glorot normal iniatializers: \(P(\phi)=\alpha\mathbf I+(1-\alpha)\mathcal N(\mathbb I;\sqrt{2\over n_{in}+n_{out}})\), where \(\mathbf I\) is an identity kernel, \(\alpha\in[0, 1]\) is a probability. Interestingly, in the official code, the kernel is initialized using glorot normal only, and with \(\alpha\) probability, it skips the random network.
Inference with Monte Carlo Approximation

Since the parameter of random networks is drawn from a prior distribution, the policy is modeled by a stochastic network: \(\pi(a\vert o;\theta)=\mathbb E_\phi[\pi(a\vert f(o;\phi);\theta)]\). To reduce variance, at the test time, an action \(a\) is taken by approximating the expectations as follows: \(\pi(a\vert o;\theta)\approx{1\over M}\sum_{m=1}^M\pi(a\vert f(o;\phi^{(m)});\theta)\), where \(M\) is the number of Monte Carlo samples. Figure3.d shows MC sampling improves the performance and reduce the variance to a noticeable extent.
Interesting Experimental Results
Comparison between PPO and PPO+random network
Figure 3.b and 3.c shows that when introducing random network to PPO, trajectories from both seen and unseen environments are aligned on the hidden space – a feature does not emerge in the plain PPO agent.
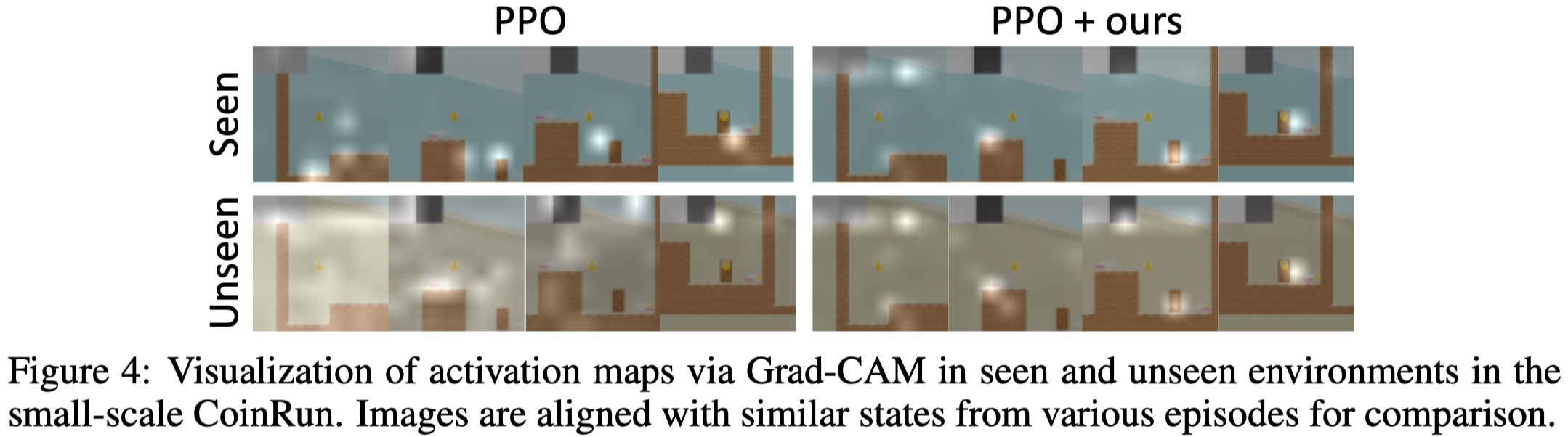
Figure 4. shows that on seen environments, both PPO and PPO+random network learns to focus on local objects. But on unseen environments, PPO failed to capture the local objects while PPO+random network still is capable of doing that.
Agents with random network in color-conditioned environments
As the random network distorts the image color, the method proposed may have trouble with color(or texture)-conditioned environments. However, some experiments in Appendix K shows that if there are other environmental factors are available to distinguish color-conditioned objects.
Poor performance on other Procgen environments
It’s been reported that network randomization works poorly on many other environments from Procgen.
References
Lee, Kimin, Kibok Lee, Jinwoo Shin, and Honglak Lee. 2019. “Network Randomization: A Simple Technique for Generalization in Deep Reinforcement Learning,” 1–22. http://arxiv.org/abs/1910.05396.

