Terminologies
Downsample/subsample: downsample refers to the reduction of signal. Examples include discretizing continuous signals and downsampling images to a lower resolution.
Aliasing: Aliasing is an effect caused by insufficient downsampling, especially when downsampling fails to capture the high-frequency signals. In that case, those high-frequency signals becomes indistinguishable and lost during downsampling. Aliasing in image downsampling results in distorted images.
Anti-aliasing: Anti-aliasing refers to techniques that minimize aliasing. A well-known anti-alising method is applying low-pass filter attenuate the high frequencies before downsampling to.
Shift-equivariance: A function \(f\) is shiftequivariant if shifting the input equally shifts the output. Let \(s\) denote a shift function that spatially shifts a image/feature map. Then \(f\) is shiftequivariant if \(s(f(x))=f(s(x))\).
Anti-aliasing with low-pass filters
Zhang 2019 shows that modern CNN architectures do not address aliasing and thus are not shift-invariant. Hence, they propose to applying low-pass filters before downsampling. Experiments shows that this method improves classification accuracy and makes the networt more stable to image perturbations and more robust to corruptions(see 4.4.2 in Zhang 2019)
Improving shift-equivariance
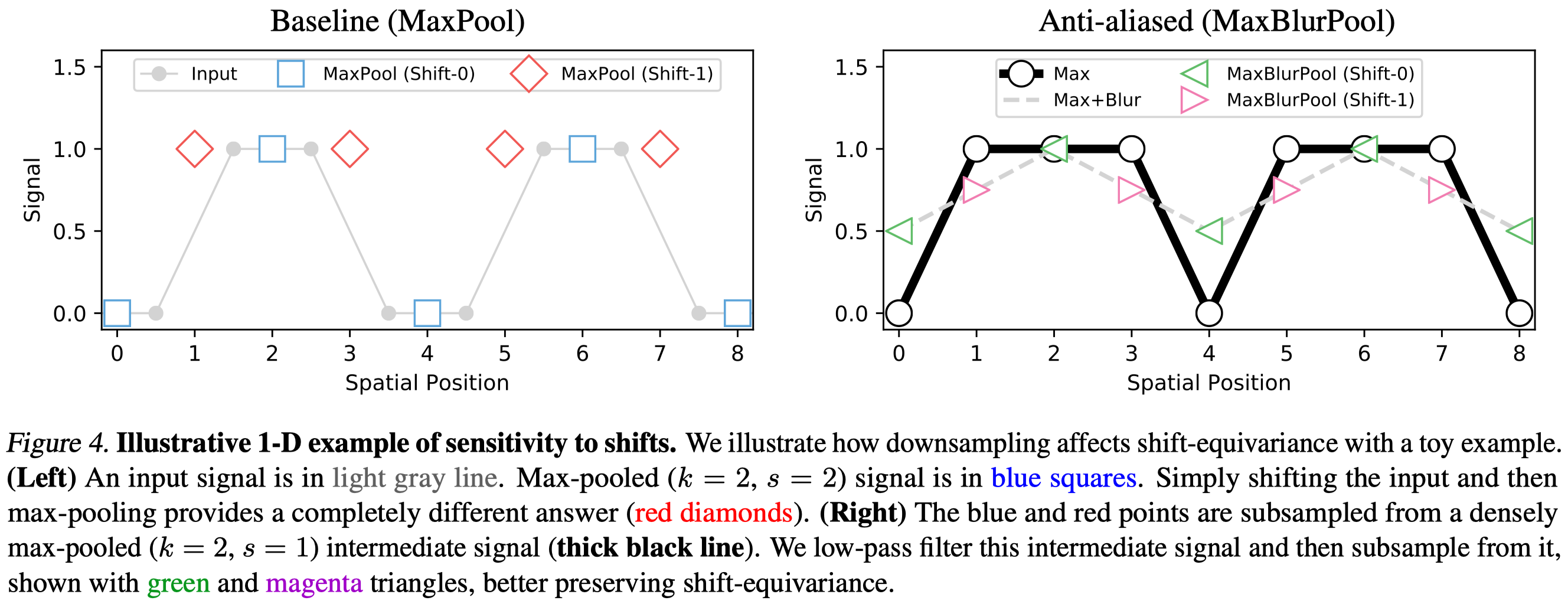
MaxPool\(\rightarrow\)MaxBlurPool. Let’s first take a look at maxpooling layer, a common method used for downsampling in computer vision. We can regard maxpooling as two successive operations: (1) evaluation the max operator densely and (2) naive subsampling. It is easy to see that the max operation preserves shift equivalence as it is densely evaluate in a sliding window fashion, but subsampling does not. Take signal in Figure 4 as an example. The original signal is \([0, 0, 1, 1, 0, 0, 1, 1]\) and its circular shifted version is \([1, 0, 0, 1, 1, 0, 0, 1]\). The max operation(kernel size = 2) results in \([0, 1, 1, 1, 0, 1, 1, 1]\) and \([1, 0, 1, 1, 1, 0, 1]\) (we apply circular padding to the rightmost) for the original and shifted signals, which demonstrates shift-equivariance. On the contrary, the subsequent subsampling(strides = 2) breaks the shift-equivariance, yielding \([0, 1, 0, 1]\) and \([1, 1, 1, 1]\).
To improve shift-equivariance, Zhang 2019 proposes to apply after the max operation a low-pass filter with kernel \(m \times m\), denoted as Blur. During implementation, bluring and subsampling are combined into a single function BlurPool.
\[\begin{align} \text{MaxPool}_{k,s}\rightarrow&\text{Subsample}_s\circ \text{Blur}_m \circ\text{Max}_k\\\ =&\text{BlurPool}_{m,s}\circ\text{Max}_k \end{align}\]where \(k\) and \(s\) are the kernel size and strides, respectively. Applying a 1D BlurPool(\(m=s=2\)) to our toy example, we get \([.5, 1, .5, 1]\) and \([.75, .75, .75,. 75]\) as shown in Figure 4 (right).
StridedConv\(\rightarrow\)ConvBlurPool. Similarly, we modify strides convolutions as follows
\[\begin{align} \text{ReLU}\circ\text{Conv}_{k,s}\rightarrow\text{BlurPool}_{m,s}\circ\text{ReLU}\circ \text{Conv}_{k, 1} \end{align}\]AveragePool\(\rightarrow\)BlurPool. For average pooling, we substitute the average operation with the blur operation.
\[\begin{align} \text{AvgPool}_{k,s}\rightarrow\text{BlurPool}_{m,s} \end{align}\]References
Zhang, Richard. 2019. “Making Convolutional Networks Shift-Invariant Again.” 36th International Conference on Machine Learning, ICML 2019 2019-June: 12712–22.

