Introduction
We discuss Agent57, the successor of NGU proposed by Badia et al. 2020, that surpasses the standard human benchmark on all 57 Atari games. In a nutshell, Agent57 makes two improvements on NGU: First, it employs a separate state-action network for the intrinsic reward, enabling the agent to learn from different scale and variance of extrinsic/intrinsic rewards. Second, it incorporates into each actor a meta-controller, typically a variant of UCB, that adaptively selects which policies to use at both training and evaluation time, making it possible to prioritize different policies during the agent’s lifetime.
State-action Value Decomposition
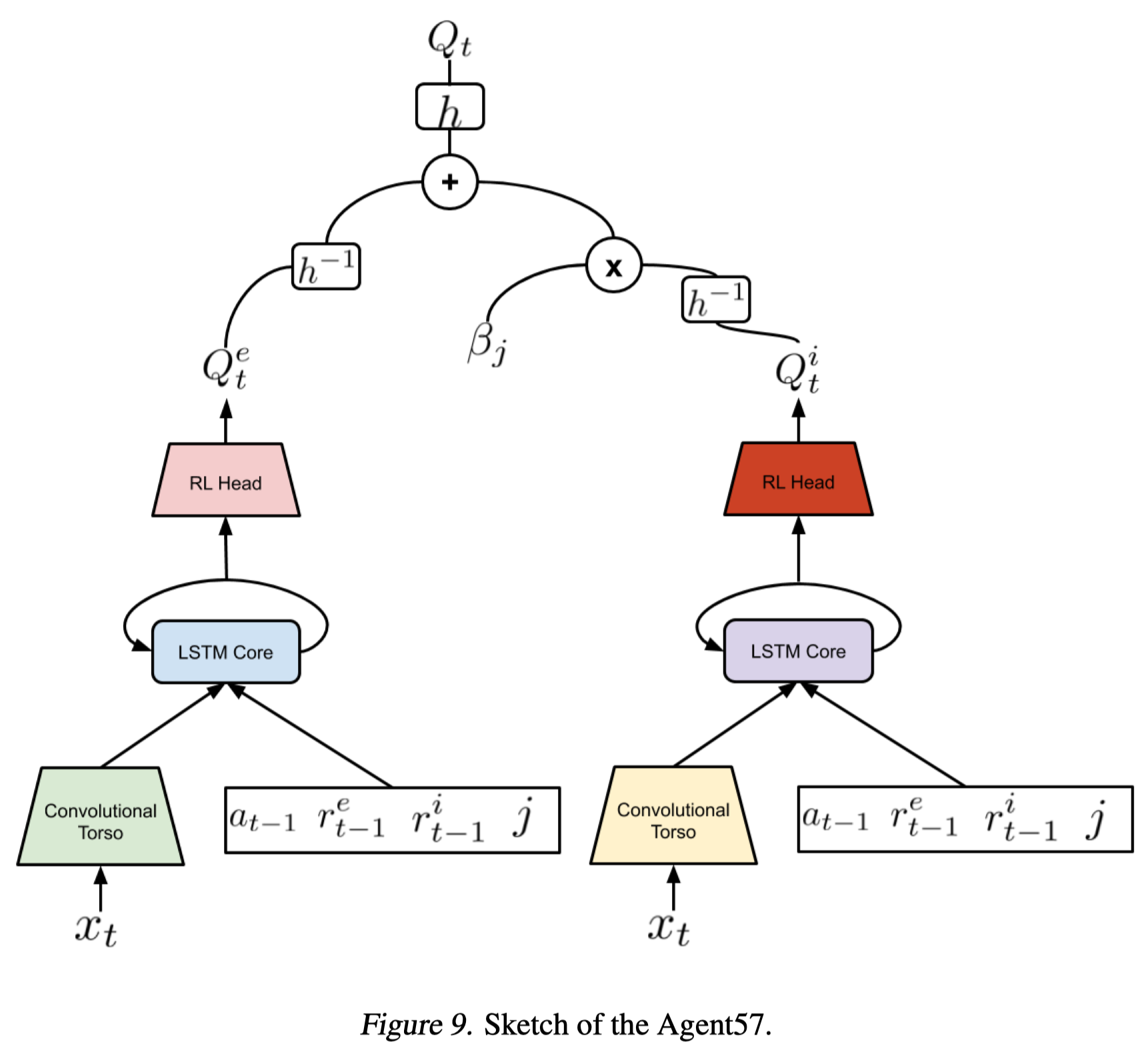
The first change made to NGU is to split the state-action value function according to intrinsic and extrinsic rewards. Formally, we represent the state-action value function as follows (also see Figure 9)
\[\begin{align} Q(x,a,i;\theta)=Q(x,a,i;\theta^e)+\beta_jQ(x,a,i;\theta^i)\tag {1} \end{align}\]where \(Q(x,a,i,\theta^e)\) and \(Q(x,a,i;\theta^i)\) are the extrinsic and intrinsic components of \(Q(x,a,i;\theta)\) respectively. This allows each network and its optimizer state to adapt to the scale and variance associated with their corresponding rewards.
Moreover, when a transformed Bellman operator is used, we can denote the state-action value function in the following way
\[\begin{align} Q(x,a,i;\theta)=h\Big(h^{-1}\big(Q(x,a,i;\theta^e)\big)+\beta_jh^{-1}\big(Q(x,a,i;\theta^i)\big)\Big)\tag {2} \end{align}\]However, in practice, Badia et al. 2020 find choosing an identity(Equation \((1)\)) or an \(h\)-transform(Equation \((2)\)) does not make any difference in terms of performance. Therefore, they simply use Equation \((1)\), but still use the transformed Retrace loss functions.
Adaptive Exploration over a Family of Policies
In NGU, all policies are trained equally, regardless of their contribution to the learning process. Badia et al. 2020 argue that this can be inefficient and propose to incorporate a meta-controller that adaptively selects which policies to use both at the training and evaluation time. Specifically, they introduce to each actor a meta controller that selects which \(Q(i)\) is used for data collection at the beginning of each episode, where \(i\) indexes the \(i^{th}\) $(\beta_i,\gamma_i)\( pair. The meta controller is a classical multi-arm bandit algorithm; specifically, Agent57 employs a sliding-window Upper Confidence Bound(UCB) with \)\epsilon_{UCB}\(-greedy exploration. That is, with probability \)\epsilon_{UCB}=0.5\(, an actor randomly selects a \)Q(i)\(; otherwise, it follows the policy of UCB. An actor computes the bound from the last \)\tau\( episodes, where we define the action value as the mean of the undiscounted extrinsic episode returns collected by running \)Q(i)\( during the last \)\tau$ episodes. Mathematically, we represent this process as follows
\[\begin{align} \begin{cases} \forall 0\le k\le N-1,&I_k=k\\\ \forall k\ge N\text{ and }U_k(0,1)\ge \epsilon_{UCB}, &I_k=\arg\max_{i}R(i,\tau)+\beta\sqrt{1\over N(i,\tau)}\\\ \forall k\ge N\text{ and }U_k(0,1)<\epsilon_{UCB}, &I_k=U(0,N-1) \end{cases}\\\ \end{align}\]where \(k\) is the \(k\)-th time an actor changes its policy/syncs its weights, \(N\) is the number of \((\beta_i,\gamma_i)\) pairs, \(U_k(0,1)\) is a random value from \([0,1]\), \(U(0,N-1)\) is a random integer from \([0,N-1]\), \(R(i,\tau)\) is the average undiscounted returns collected using \(Q(i)\) in the last \(\tau=160\) episodes, and \(N(i,\tau)\) is the number of times \(Q(i)\) is selected in the last \(\tau\) episodes.
Notice that Agent57 associates each actor with a meta-controller, as opposed to a global meta-controller. This is because each actor follows a different \(\epsilon_l\)-greedy policy which may alter the choice of the optimal policy.
Tackling The Long-term Credit Assignment Problem
NGU fails to cope with long-term credit assignment problems such as Skiing, in which the reward, given only at the end, is proportional to the time elapsed. Agent57 tackles the long-term credit assignment problem with a combination of adaptive training schedule, larger discount factor, and increasing the backprop through time window. As we have discussed the adaptive training schedule in the previous section, we discuss the remaining two next.
The discount factor now increases up to \(0.9999\) and is scheduled as follows(also see Figure 11 for illustration)
\[\begin{align} \gamma_i=\begin{cases} \gamma_0&\text{if }i=0\\\ \gamma_1+(\gamma_0-\gamma_1)\sigma(10{2i-6\over 6})&\text{if }i\in\{1\dots6\}\\\ 1-\exp\left((N-9)\log(1-\gamma_1)+(i-8)\log(1-\gamma_2)\over N-9\right) \end{cases}\\\ where\ \gamma_0=0.9999, \gamma_1=0.997,\gamma_2=0.99 \end{align}\]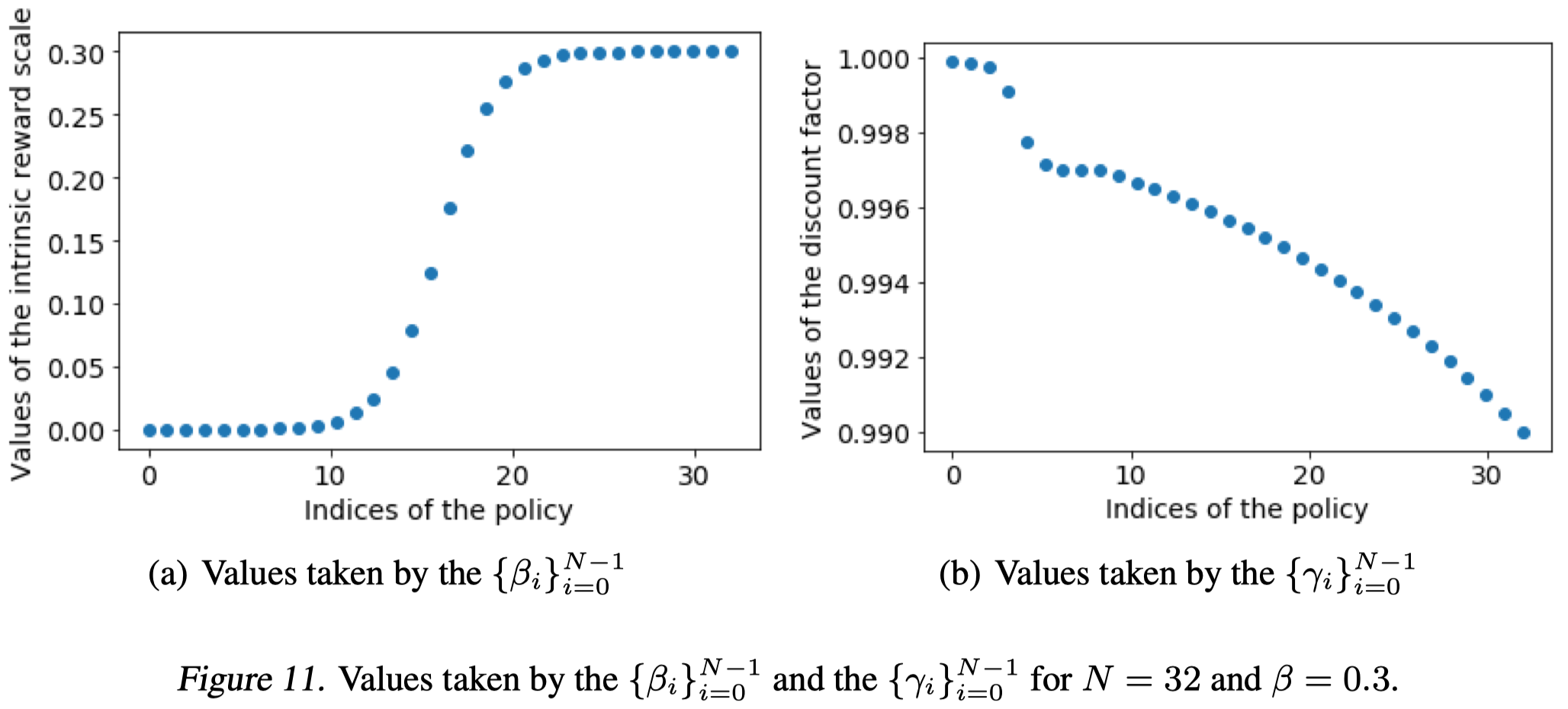
The intuition is the same as NGU: we want the exploitative policies equipped with high discount values and explorative policy with small discount values.
Agent57 doubles the backprop through time window from sizes of 80 to sizes of 160. Experiments show that a longer backprop through time window results in better overall stability and slightly higher final score although it’s initially slower.
Experimental Results
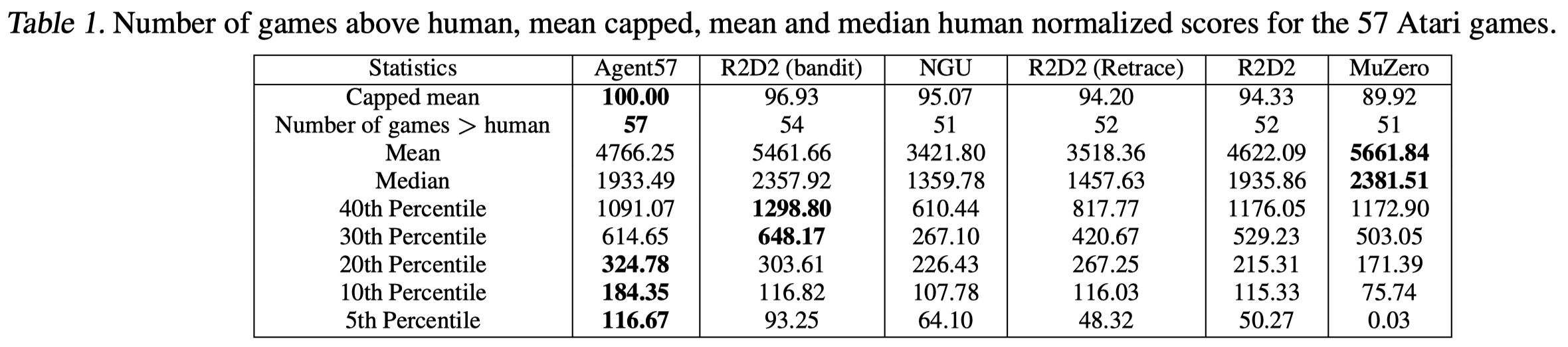
We can see from Table 1 that Agent57 outperforms other methods up to the 20th percentile, showing the generality of Agent57. Also notice that the meta-controller improvement successfully transfers to R2D2, in which we use different discount factors for different policies. Furthermore, The meta-controller allows to include very high discount values in the set. Specifically, running R2D2 with a high discount factor, \(\gamma=0.9999\) surpasses the human baseline in the game of Skiing. However, using that hyperparameter only across the training time renders the algorithm very unstable and damages its final performance.
References
Badia, Adrià Puigdomènech, Bilal Piot, Steven Kapturowski, Pablo Sprechmann, Alex Vitvitskyi, Daniel Guo, and Charles Blundell. 2020. “Agent57: Outperforming the Atari Human Benchmark.” http://arxiv.org/abs/2003.13350.

