Introduction
Self-imitation learning has been shown to improve policy learning and sample efficiency by exploiting past successful policies. However, the exploitation of good experiences within limited directions might hurt performance in some cases if the good experiences lead to a suboptimal solution deviating from the optimal one. In this post, we discuss Diverse Trajectory-conditioned Self-Imitation Learning (DTSIL), proposed by Guo et al. 2021, that addresses the above problem by imitating a diverse of past experiences and random exploration after the imitation is done.
Trajectory Buffer
We assume the environment provides a state feature/embedding \(e_t\) in addition to the observation \(o_t\) and maintain a trajectory buffer \(\mathcal D={(e^{(i)},\tau^{(i)}, n^{(i)})}\) of diverse past trajectories, where \(\tau^{(i)}\) is the best trajectory ending with a state with feature \(e^{(i)}\), \(n^{(i)}\) is the number of times the cluster represented by the embedding \(e^{(i)}\) has been visited during training. For a new feature \(e_t\), if it’s close to a feature \(e^{(i)}\) in the buffer, i.e., the Euclidean distance is within a threshold \(\delta=0.1\), we increase the count \(n^{(i)}\). Moreover, if the sub-trajectory \(\tau_{\le t}\) of the current episode is better than \(\tau^{(i)}\) in terms of cumulative rewards or length of the sub-trajectory, we replace \(\tau^{(i)}\) with \(\tau_{\le t}\) and \(e^{(i)}\) with \(e_t\). If \(e_t\) is not sufficiently similar to any state embedding in the buffer, a new entry \((e_t,\tau_{\le t}, 1)\) is added to the buffer.
Sampling for Exploitation and Exploration
With probability \(1-p\), we sample a demonstration in the buffer with the highest cumulative rewards for exploitation. With probability \(p\), we sample a demonstration with probability proportional to \(1/\sqrt{n^{(i)}}\) for exploration.
Architecture
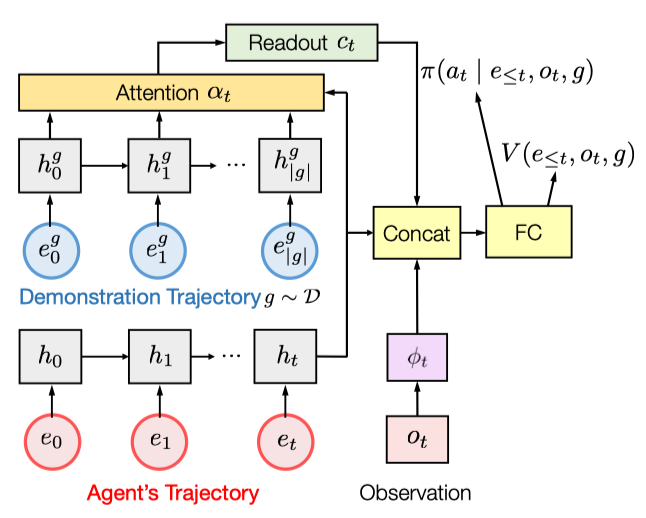
The network bears much resemblance to a neural machine translation model that combines a sequence-to-sequence model with an attention mechanism. The RNN encoder computes the hidden states \(h^g_{0:\vert g\vert }\) for the state features \(e_t\) from a demonstration trajectory, while the RNN decoder computes the hidden states \(h_{0:t}\) for the state features from the current trajectory. An attention module compares \(h_t\) with \(h_{0:\vert g\vert }^g\), producing readout \(c_t\), the attention-weighted summation of \(h_{0:\vert g\vert }^g\).
The policy and the state value are computed by MLPs where the input is the concatenation of the readout \(c_t\), the decoder hidden states \(h_t\), and the observation embedding \(\phi_t(o_t)\).
Objectives
Reinforcement Learning Objective
Given a demonstration trajectory \(g={e_0^g, e_1^g,\dots,e_{\vert g\vert }^g}\), we provide rewards for imitating \(g\) and train the policy to maximize rewards. At the beginning of an episode, the index \(u\) of the lastly visited state feature in the demonstration is initialized as \(u=-1\). At each step \(t\), if the agent’s new state feature \(e_{t+1}\) is similar enough to any of the next \(\Delta t\) state features \(e_{u:u+\Delta t}^g\)(i.e., \(\Vert e_{t+1}-e_{u’}^g\Vert <\delta\) where \(u<u’\le u+\Delta t\)), it receives a positive reward \(r^{DTSIL}_t\), and \(u\) is updated to \(u’\). Otherwise, the reward \(r_t^{DTSIL}\) is zero. This encourages the agent to visit the state embeddings in the demonstration in a soft-order so that the agent could possibly edit or augment the demonstration when executing a new trajectory. In summary, the reward \(r_t^{DTSIL}\) is defined as
\[\begin{align} r_t^{DTSIL}=\begin{cases} f(r_t)+r^{im}&\text{if }\exists u',u< u'\le u+\Delta t \text{ such that }\Vert e_{u'}^g-e_{t+1}\Vert <\delta\\\ 0&\text{otherwise} \end{cases} \end{align}\]where \(f(r_t)\) is a monotonically increasing function(e.g., the clipping function in Atari games), \(r^{im}\) is the imitation reward with a value of \(0.1\) in experiments.
With \(r_t^{DTSIL}\), the trajectory-conditioned policy is trained with a policy gradient algorithm such as PPO.
Supervised Learning Objective
For a demonstration trajectory \(\tau={(o_0,e_0,a_0,r_0),(o_1,e_1,a_1,r_1),\dots}\), DTSIL also maximizes the log likelihood of taking \(a_t\) at time step \(t\):
\[\begin{align} \mathcal L^{SL}=-\log\pi(a_t|e_{\le t}, o_t,g) \end{align}\]However, there is no ablation study of the effect of this objective.
Random Exploration
The agent acts according to the learned policy until the last state of the demonstration is achieved. After that, the agent act randomly until the episode ends.
Effects of Hyperparameters
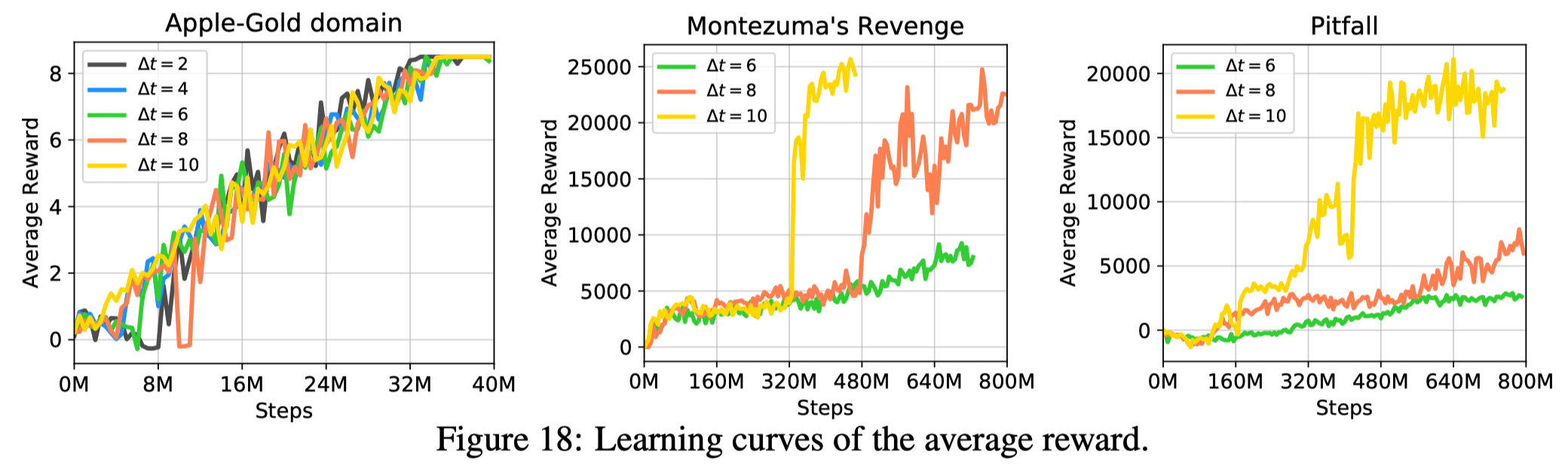
Figure 18 shows that \(\Delta t\) plays a non-trivial role in the agent’s performance. A large \(\Delta t\) provides more flexible for the agent to visit any of the next \(\Delta t\) future state while \(\Delta t\) requires the agent to exactly mimic the demonstration.
References
Guo, Yijie, Jongwook Choi, Marcin Moczulski, Shengyu Feng, Samy Bengio, Mohammad Norouzi, and Honglak Lee. 2021. “Memory Based Trajectory-Conditioned Policies for Learning from Sparse Rewards.” NeurIPS 2020, no. NeurIPS: 1–13. http://arxiv.org/abs/1907.10247.

