Introduction
We discuss an exploration method, namely episodic curiosity(EC), that computes intrinsic rewards based on the novelty of the current observation compared to those in its episodic memory. In a nutshell, EC trains a siamese network that predicts whether the current observation is reachable from some previous states in \(K\) steps, based on which, it derives an intrinsic reward for the current state. Experimental results shows this method is able to overcome the noisy TV problem and outperforms ICM in all the test environments.
R-Network
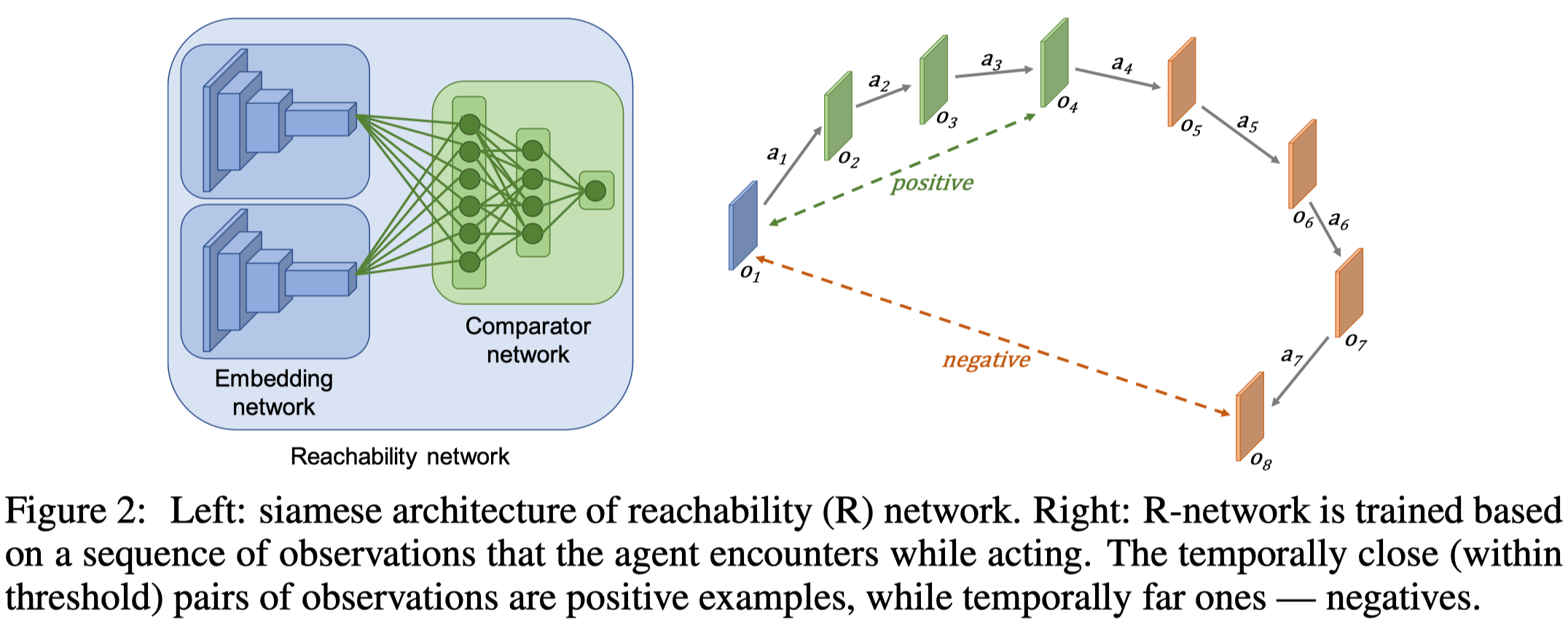
EC uses a siamese architecture to compute the intrinsic reward. The architecture, which is called Reachability network or \(R\)-network for short, consists of two sub-networks: an embedding network \(E:\mathcal O\rightarrow \mathbb R^n\) that encodes images into a low dimensional space, and a comparator network \(C:\mathbb R^n\times \mathbb R^n\rightarrow [0,1]\) that outputs the probability of the current observation being reachable from the one we compared with in \(K\) steps(see Figure 2 left).
Computing Intrinsic Bonus
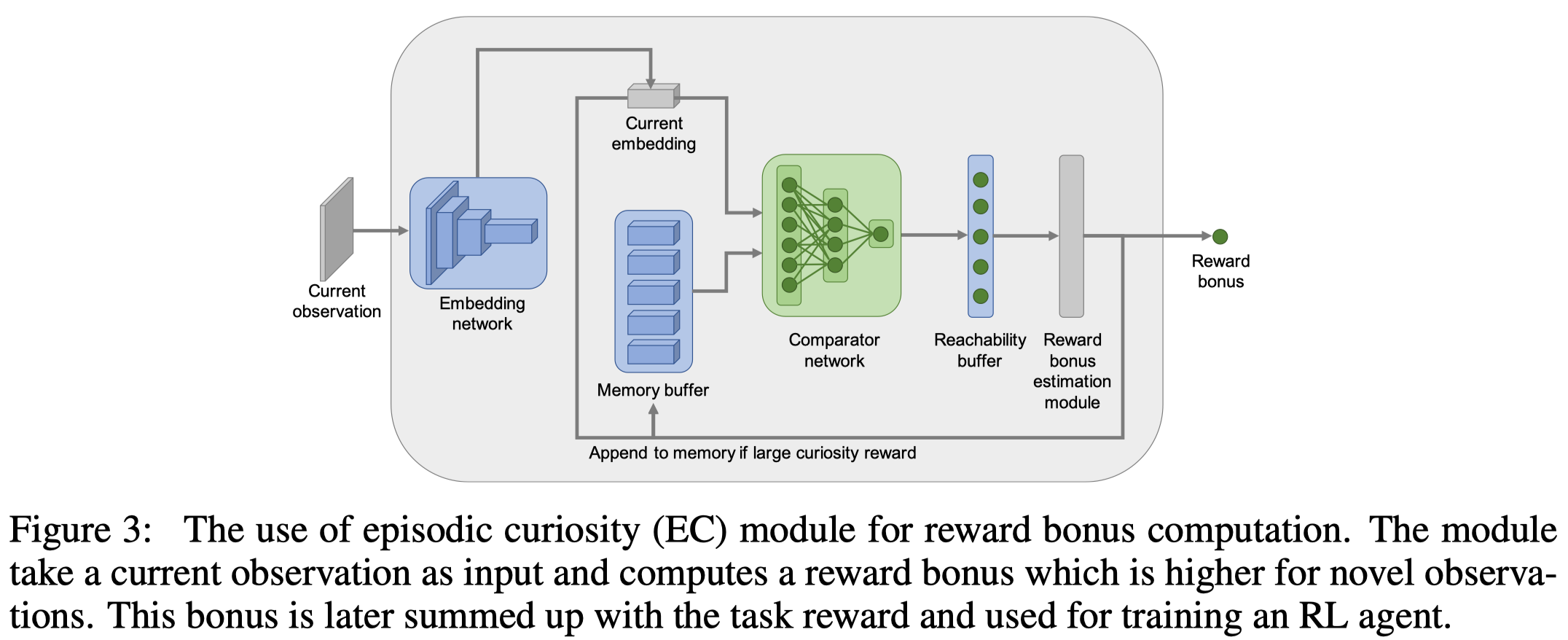
Whenever a new observation is received, we first embed it through the embedding network \(E\). Then we compare the embedding \(e\) with all the previous embeddings stored in the episodic memory buffer \(M\) using the comparator network \(C\). This produces \(\vert M\vert =200\) values \(c_1, \dots, c_{\vert M\vert }\), from which we compute a similarity score as follows
\[\begin{align} C(M,e)=F(c_1,\dots,c_{|M|}) \end{align}\]where \(F\) computes the \(90\)-th percentile—we choose this instead of the maximum as it’s robust to outliers. We compute a curiosity bonus \(b\) in the following way
\[\begin{align} b=\alpha(\beta-C(M,e)) \end{align}\]where \(\alpha\in \mathbb R^+\) controls the scale of the intrinsic reward, and \(\beta\) determines the sign of the reward. Empirically, \(\beta=0.5\) works well for fixed-duration episodes, and \(\beta=1\) is preferred if an episode could have variable length.
The observation embedding is added to memory if the bonus \(b\) is larger than a novelty threshold \(b_{bonus}\).
Training R-Network
We generate inputs to the R-network from a sequence of observations \(o_1,\dots,o_N\). We first sample an anchor observation \(i\), then we sample some \(\vert i-j\vert \le k\) as its positive example and some \(\vert i-j\vert > \gamma k\) as its negative example. The hyperparameter \(\gamma\) is used to create a gap between positive and negative examples. However, there is little clue how to select this value from the paper. The network is trained with logistic regression loss to output the probability of the reachable class.
Interesting Experimental Results
They found training R-network and PPO at the same time performs better than training it offline.
Generalization
In supplementary S4, Savinov et al. shows R-network transfers reasonably well from one task to another in most experiments.
Importance of Embedding and Comparator Networks
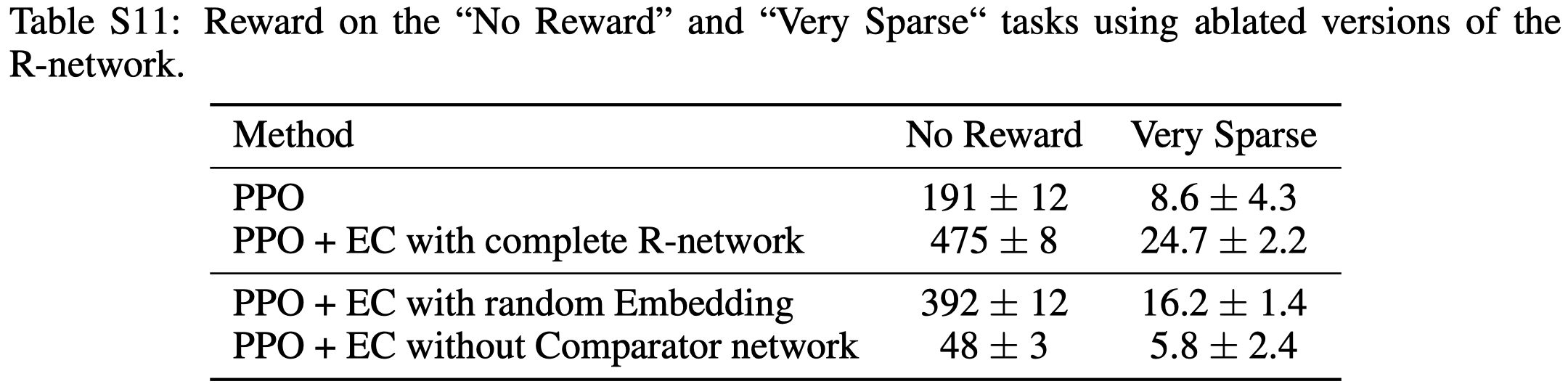
Table S11 shows that training embedding network improves the performance but it’s not neccessary. On the other hand, when training without the Comparator network, where we train the embeddings with \(\sigma(e_1^\top e_2)\), the quality drops below the plain PPO, showing the comparator plays a non-trivial role in the architecture.
Improving R-Network by Un-Shared Siamese Branches
The authors also experiments with a un-shared siamese branches that use different embedding networks for the anchor and target inputs significantly improves the prediction accuracy and allows to use a simple comparator \(\sigma(e_1^\top e_2)\). One superficial explanation is that this unshared branches R-network implements a strictly larger family of functions.
References
Savinov, Nikolay, Anton Raichuk, Raphaël Marinier, Damien Vincent, Marc Pollefeys, Timothy Lillicrap, and Sylvain Gelly. 2019. “Episodic Curiosity through Reachability.” 7th International Conference on Learning Representations, ICLR 2019, 1–20.
Code: https://github.com/google-research/episodic-curiosity/blob/3c406964473d98fb977b1617a170a447b3c548fd/third_party/keras_resnet/models.py#L328

