Model-Based Meta-Policy Optimization
Model-based RL algorithms generally suffer the problem of model bias. Much work has been done to employ model ensembles to alleviate model-bias, and whereby the agent is able to learn a robust policy that performs well across models. The downside of these methods is obvious: policies learned to be robust across models often tend to be over-conservative, especially in regions where models disagree. In contrast, Clavera et al. in 2018 proposed to apply MAML to an ensemble of learned dynamics models so that the agent meta-learns a policy that is robust in regions where the models agree, and adaptive where the models yield substantially different predictions. In their experiments, the resulting method, namely Model-Based Meta-Policy Optimization(MB-MPO), is able to achieve asymptotic performance of model-free methods while being substantially more sample efficient.
The central idea of MB-MPO is simple: it learns \(K\) dynamics models and meanwhile meta-learns a policy over these models through MAML.
Model Learning
In MB-MPO, we learn an ensemble of dynamics models \({\hat f_{\phi_k}}\), where \(\hat f_{\phi_k}(s_t,a_t)=\hat s_{t+1}-s_t\). Each model minimizes the \(\ell_2\) one-step prediction loss:
\[\begin{align} \min_{\phi_k}\mathbb E_{(s_t,a_t,s_{t+1})\sim\mathcal D}\left\Vert s_{t+1}-\left(\hat f_{\phi_k}(s_t,a_t)+s_t\right)\right\Vert_2^2 \end{align}\]Standard techniques to avoid overfitting and facilitate fast learning are followed; specifically, 1) early stopping the training based on the validation loss, 2) normalizing the inputs and outputs of the neural network, and 3) weight normalization
Algorithm
The algorithm bears much resemblance to MAML-RL, except that the agent here meta-learns a policy over the learned dynamics models rather than over a set of real tasks.

where the gradient in step \(7\) is computed through vanilla policy gradient(VPG), while step \(10\) employs trust-region policy optimization(typo, it’s supposed to be an addition). Note that, in step \(3\), MB-MPO samples trajectories using adapted policies instead of the updated policy. This increases the diversity of training data \(\mathcal D\) and thereby improves the quality of model learning.
Benefits of The Algorithm
Regularization effect during training. Optimizing the policy to adapt within one policy gradient step to any of the fitted models imposes a regularizing effect on the policy learning. The meta-optimization problem steers the policy towards higher plasticity in regions with high dynamics model uncertainty, shifting the burden of adapting to model discrepancies towards the inner policy gradient update(step \(7\) in the algorithm).
Tailored data collection for fast model improvement. As we stated before, MB-MPO sample trajectories using adapted policies to increase the diversity of the training data which promotes robustness of the dynamics models. Specifically, the adapted policies tend to exploit the characteristics deficiencies of the respective dynamics models.
Fast fine-tuning. The policy is learned to be adaptive for a set of belief dynamics. This frees the need for an accurate global model, making the policy more robust in real environment.
Experimental Results
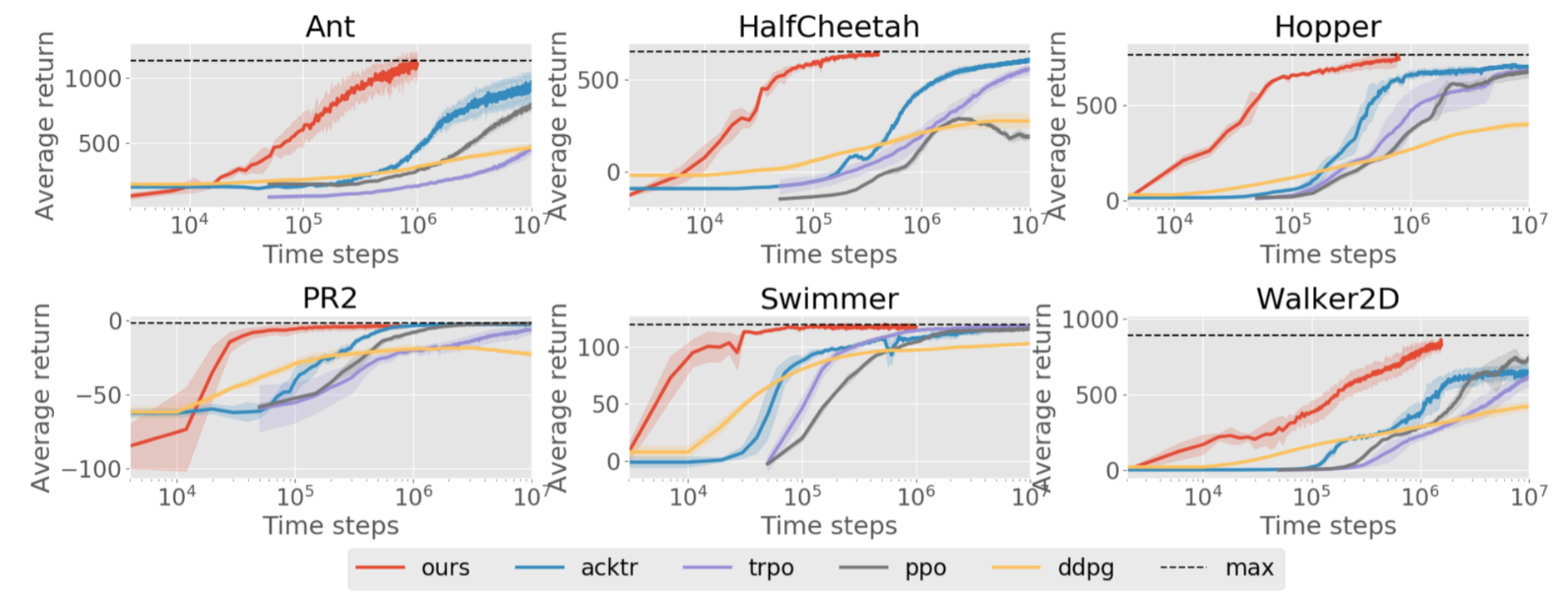
Surprisingly, this method works extremely well in Mujoco environments
Supplementary Materials
Weight Normalization
In weight normalization, we parameterize the weight vectors(not weight matrix) using
\[\begin{align} \mathbf w={g\over\Vert\mathbf v\Vert}\mathbf v \end{align}\]where \(g\) is a learnable scalar and \(\mathbf v\) a learnable vector. Weight normalization seperates the norm of the weight vector from its direction without reducing expressiveness
Here’s a code reference from Open AI.
References
Clavera, Ignasi, Jonas Rothfuss, John Schulman, Yasuhiro Fujita, Tamim Asfour, and Pieter Abbeel. 2018. “Model-Based Reinforcement Learning via Meta-Policy Optimization.” CoRL, no. CoRL. http://arxiv.org/abs/1809.05214.

