Introduction
We discuss the effect of regularizations in neural networks in policy optimization on continuous control tasks.
TL; DR
- Apply \(L_2={1\over 2}\lambda\Vert \theta\Vert_2^2\) with \(\lambda\) around \(1e-4\) to the policy network.
- Regularization is more effective on the policy than that on the value function.
- Regularization helps policy to generalize from seen samples to unseen ones
- For on-policy algorithms, simple regularizations, such as \(L_2\), \(L_1\), and weight clipping, significantly boost performance, to the extent sometimes even more significant than entropy bonus.
- Regularizations are more effective in challenging tasks
- \(L_2\) regularization is the most effective regularization across algorithms and environments
- Batch normalization and dropout can only help in off-policy algorithms sometimes.
Settings
Liu et al. 2021 study six regularizations, namely \(L_2\), \(L_1\) regularization, weight clipping, dropout, batch normalization, and entropy regularization on nine continuous control tasks. Tasks are categorized into two groups: easy and hard. Without explicit specification, experiments are obtained by only regularizing the policy. Regularizations are evaluated separately; no combination is concerned. We are especially interested in comparing network regularization techniques (the first five) to the entropy regularization.
We say the performance is improved if \(\mu_{env, r}-\sigma_{env, r}>\max(\mu_{env,b}, T(env))\), where \(\mu_{env,r},\sigma_{env,r}\) are the mean and standard deviation of returns over five seed, \(\mu_{env,b}\) is the baseline mean return, \(T(env)\) is the minimum return threshold of an environment. We say the performance is hurt if \(\mu_{env, r}-\sigma_{env, r}<\mu_{env,b}\).
Comparisons
Policy and Value Network Regularization
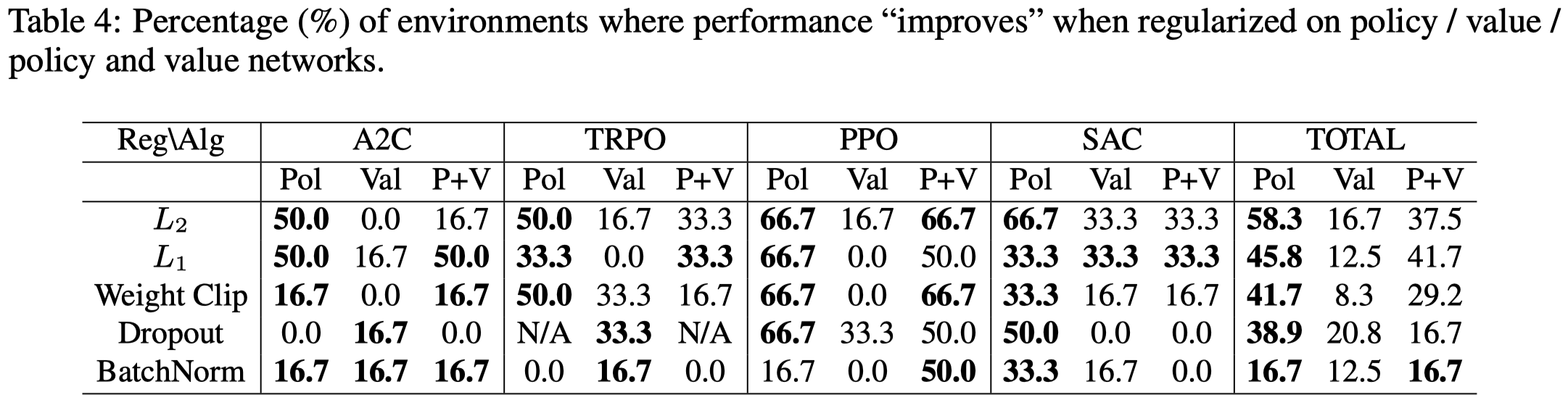
Table 4 shows that regularizations are more effective in the policy than the value function. Potential explanation is that regularizations help policy to generalize from seen samples to unseen ones—the generalization mentioned in this post only indicates the ability to generalize to unseen samples but not unseen environments.
Efficacy of Different Regularizations
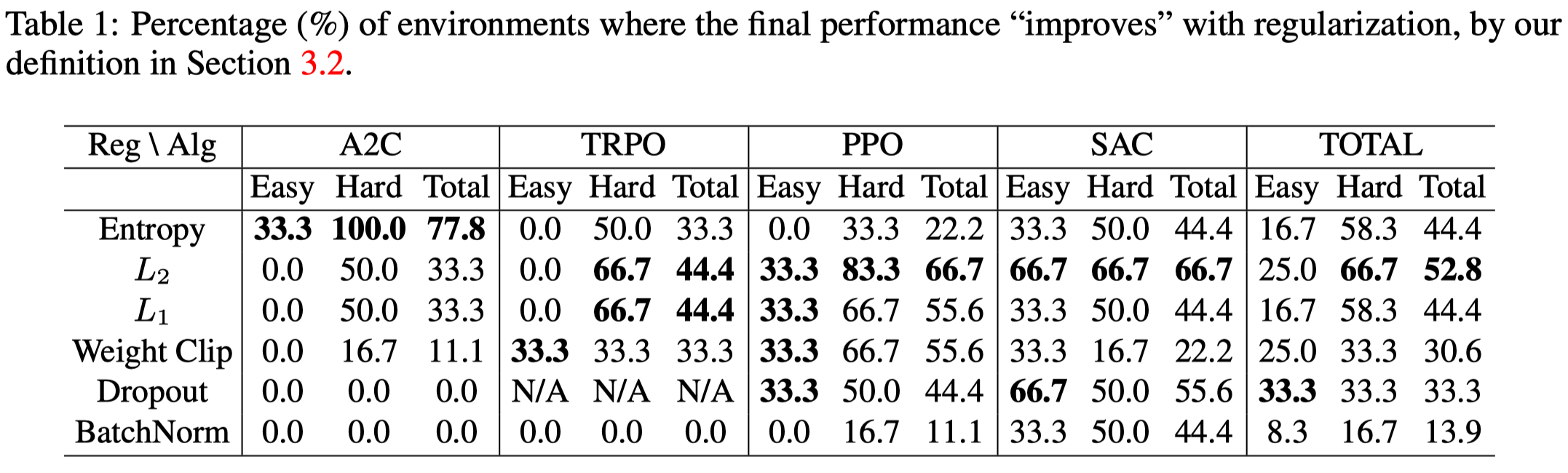
Table 1 shows:
- \(L_2\) is the most effective regularization across algorithms and environments and overall, it’s more effective than entropy regularization.
- BN and dropout in general hurt in on-policy algorithms but help in off-policy algorithms. Possible explanations are 1) BN and dropout are treated different in training and evaluation, leading to a discrepancy between the sampling policy and optimization policy. 2) BN can be sensitive to input distribution shifts since the statistics depend on the input. If the input distribution changes too quickly, the mapping functions of BN layers can change quickly too, which can possibly destabilize training. This happens to on-policy algorithms as samples are always generated from the latest policy. In off-policy algorithms, the sample distribution are relatively slow-changing due to the introduction of the experience replay.
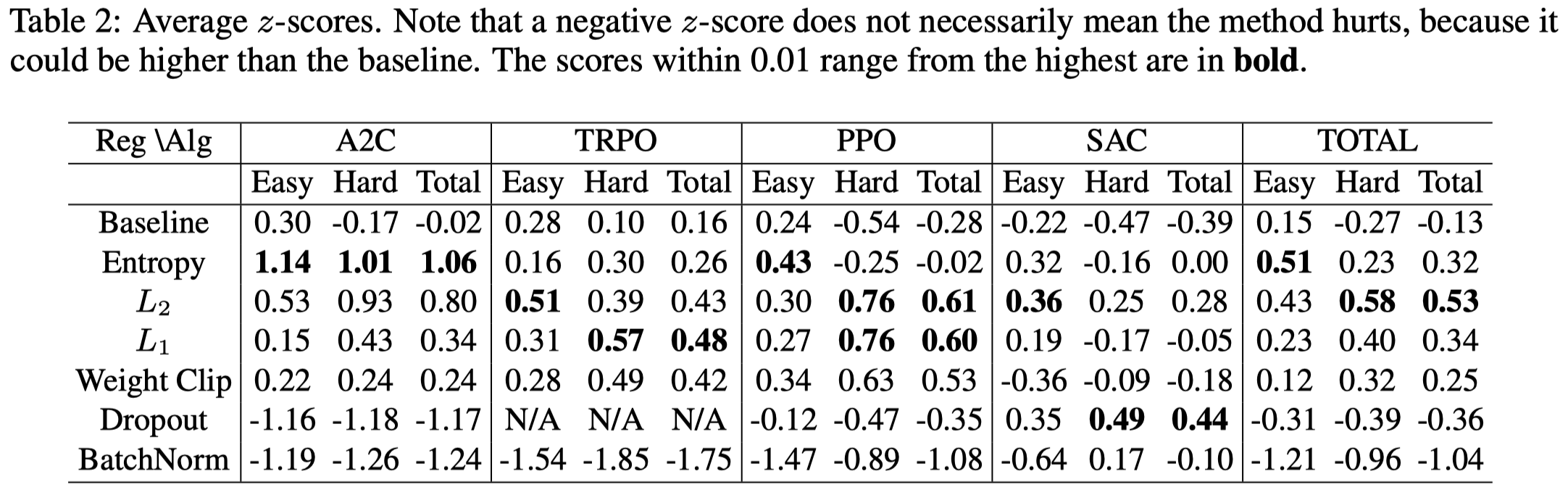
Table 2 shows how much each regularization improves the performance, measured in \(z\)-score. We can see
- \(L_2\) tops the average \(z\)-score most often
- \(L_2\), \(L_1\) and weight clipping is more effective than entropy regularization in PPO on hard tasks
Analysis
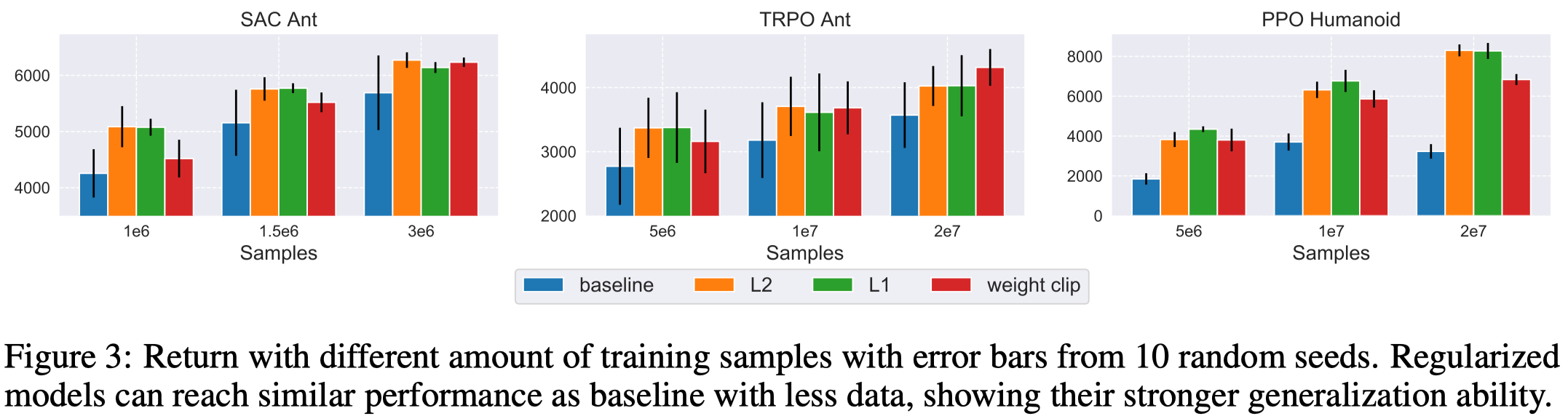
Figure 3 shows sample efficiency is improved when regularizations are applied, verifying regularizations improve the policy generalization ability.
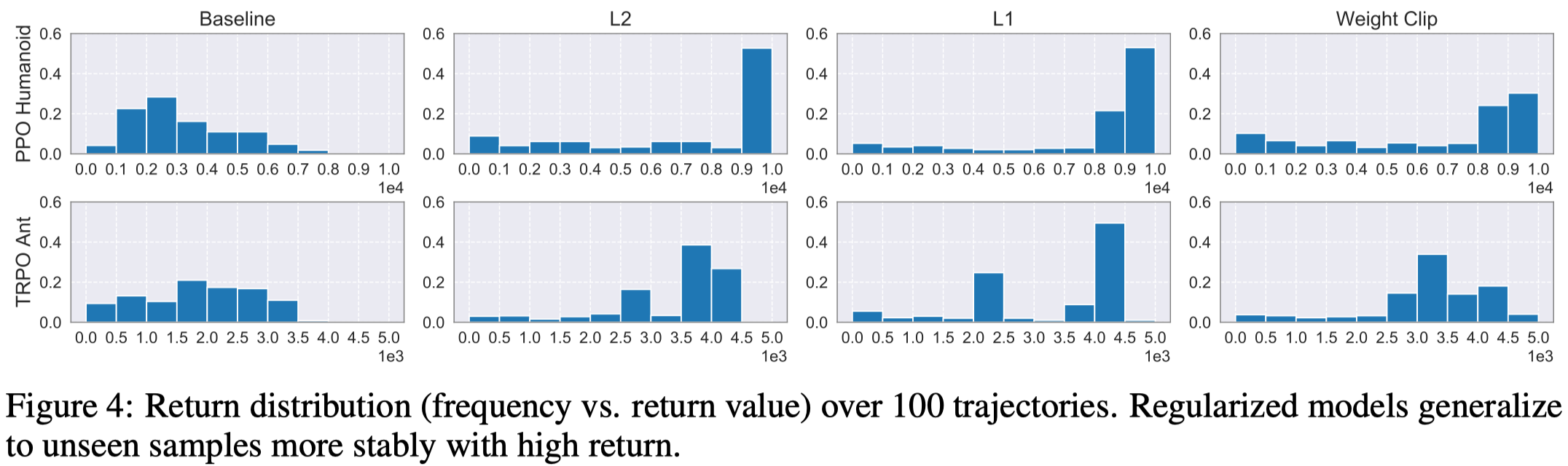
Figure 4 shows regularized models exhibit better performance at evaluation, usually of less variance and more concentrated on high returns.
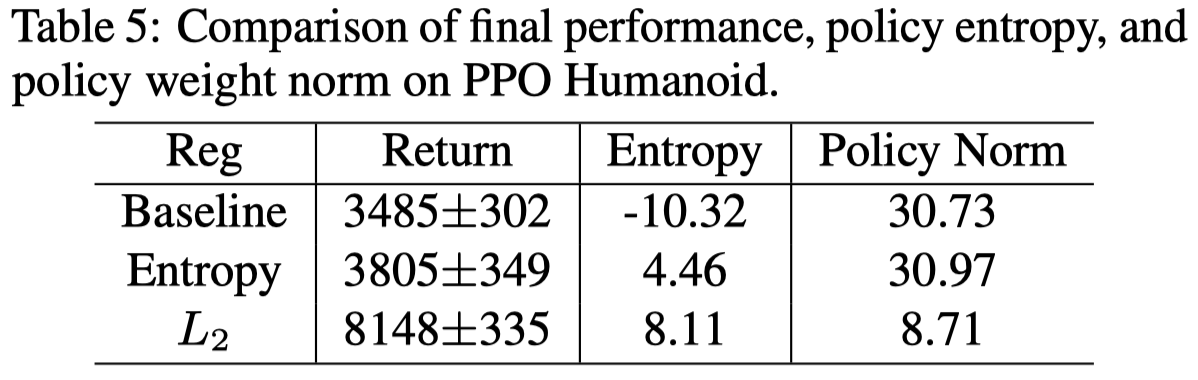
Table 5 shows \(L_2\) limits the policy norm, improves the policy entropy, and exhibit better performance on hard tasks Humanoid. We conjecture that small weight norm makes the network less prone to overfitting and provide a better optimization landscape for the model
References
Zhuang, Liu, Xuanlin Li, Bingyi Kang, and Trevor Darrell. 2021. “Regularization Matters in Policy Optimization - An Empirical Study on Continuous Control.” Iclr2021, no. Ii: 1–26.
Supplementary Materials
\(z\)-score
\(z\)-score is the signed fractional number of standard deviations by which the value of a data point is above the mean, i.e., \(z=\mathbb E[(x-\hat\mu)/{\hat\sigma}]\), where \(\hat\mu\) and \(\hat\sigma\) is the sample mean and standard deviation of returns over five seeds across all algorithms.

