Introduction

We discuss Deep Planning Network(PlaNet), a model-based agent that achieve comparable performance on a variety of image-based control tasks. In a nutshell, PlaNet learns a dynamics through the recurrent state space model and uses model-predictive control(MPC) with cross entropy method(CEM) for action selection.
Dynamics Learning
A traditional dynamics model can be divided into three parts
\[\begin{align} &\text{Transition model:}&s_t\sim p(s_t|s_{t-1}, a_{t-1})\\\ &\text{Observation model:}&o_t\sim p(o_t|s_t)\\\ &\text{Reward model:}&r_t\sim p(r_t|s_t) \end{align}\]where all models are parameterized by (de)convolutional/fully-connected networks with Gaussian heads. We can train these models using MSE but this can easily lead to overfitting. Instead, Hafner et al. propose to use a variant of VAE structure with an additional encoder \(q(s_{1:T}\vert o_{1:T}, a_{1:T})=\prod_{t=1}^Tq(s_t\vert s_{t-1},a_{t-1},o_t)\) serving as the posterior, where \(q(s_t\vert s_{t-1},a_{t-1},o_t)\) is a convolutional network followed by a feed-forward network with a Gaussian head. The four networks are trained jointly with the variational evidence lower bound(ELBO) defined below
\[\begin{align} \mathbb E\left[\sum_t\log q(o_t|s_t)+\log q(r_t|s_t)\right]-\mathbb E\left[\sum_t D_{KL}\left[p(s_t|s_{t-1},a_{t-1},o_t)\Vert q(s_t|s_{t-1},a_{t-1})\right]\right] \end{align}\]Recurrent State-Space Model
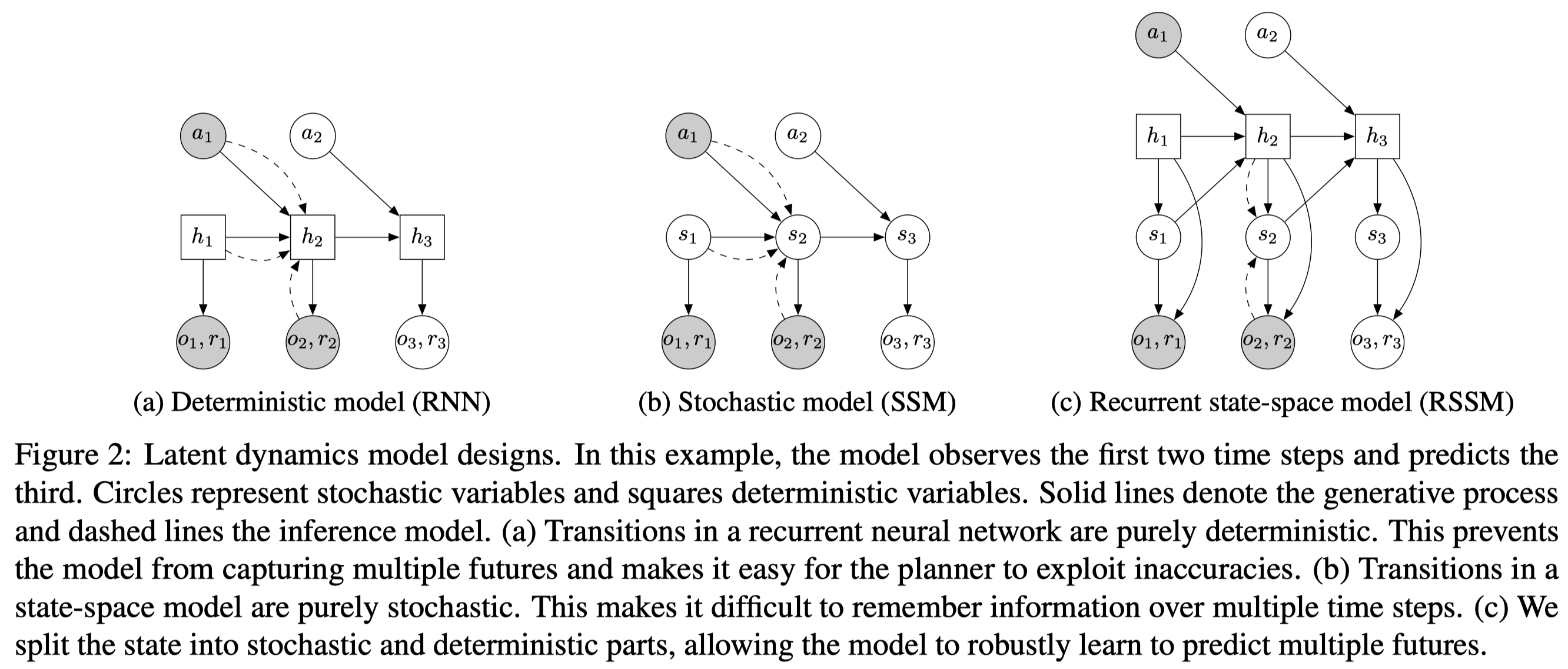
The dynamics model we discussed before is general, but it lacks the ability to reliably remember information across steps. In theory, this model could learn to set the variance to zero for some state components, but the optimization procedure may not find this solution. This motivates including a deterministic module such as an RNN. Figure 2c demonstrates the resulting model, recurrent state-space model(RSSM), which can be mathematically expressed as
\[\begin{align} &\text{Deterministic state model:}&h_t=f(h_{t-1},s_{t-1},a_{t-1})\\\ &\text{Stochastic state model:}&s_t\sim p(s_t|h_t)\\\ &\text{Observation model:}&o_t\sim p(o_t|h_t,s_t)\\\ &\text{Reward model:}&r_t\sim p(r_t|h_t,s_t) \end{align}\]where \(f\) is an RNN. We also change the posterior to \(q(s_{1:T}\vert o_{1:T},a_{1:T})=\prod_{t=1}^Tq(s_t\vert h_t,o_t)\) accordingly, in which we move the time-dependency to \(h\) as the stochastic state model does. The following figure demonstrates operations in an RSSM cell, where \(e_t\) is the image embedding, \(s\) and \(s’\) are the outputs of the prior \(p\) and posterior \(q\), respectively.

Latent Overshooting
Hafner et al. also propose latent overshooting which generalizes standard 1-step ELBO to multi-step version. We omit this and refer interested readers to the paper as it is not found to be useful in practice.
Planning

PlaNet searches for the best action at time step \(t\) using cross entropy method(CEM), which is selected because of its robustness and because it solved all considered tasks when given the true dynamics for planning. CEM is a population-based optimization algorithm that infers a distribution over action sequences that maximize the objective. As detaied in Algorithm 2, the policy \(q\) starts with a diagonal Gaussian belief \(\mathcal N(0,\mathbb I)\). For each iteration, we repeatedly sample \(J\) action sequences using the current policy belief \(q\)(Lines 4-5), evaluate them under the model(Line 6), and refit the policy belief to the top \(K\) sequence(Lines 7-9).
The evaluation is simply done in the state space using rewards collected in steps \([t:t+H]\) as shown in Line 6. This is sufficient as CEM is a population-based algorithm.
References
Danijar Hafner, Timothy Lillicrap, Ian Fischer, Ruben Villegas, David Ha, Honglak Lee, James Davidson. Learning Latent Dynamics for Planning from Pixels. In ICML 2019

