Introduction
QMIX is a value-based algorithm for multi-agent settings. In a nutshell, QMIX learns an agent-specific \(Q\) network from the agent’s local observation and combines them via a monotonic mixing network whose weights are generated by some hypernetworks with an absolute activation in the end.
Assumption
QMIX is built upon the assumption that a global \(\arg\max\) performed on \(Q_{tot}\) yields the same result as a set of individual \(\arg\max\) operations performed on each \(Q_a\). To this end, it’s sufficient (but not necessary) to enforce a monotonicity constraint on the relationship between \(Q_{tot}\) and each \(Q_a\)
\[\begin{align} {\partial Q_{tot}\over\partial Q_a}\ge 0\quad \forall a \end{align}\]In other words, we expect \(Q_{tot}\) at least do not decreases when \(Q_a\) increases.
Note that this assumption does not always hold. In cases where an agent’s decision should be made according to other agents’ action at the same time step, this assumption breaks.
Method
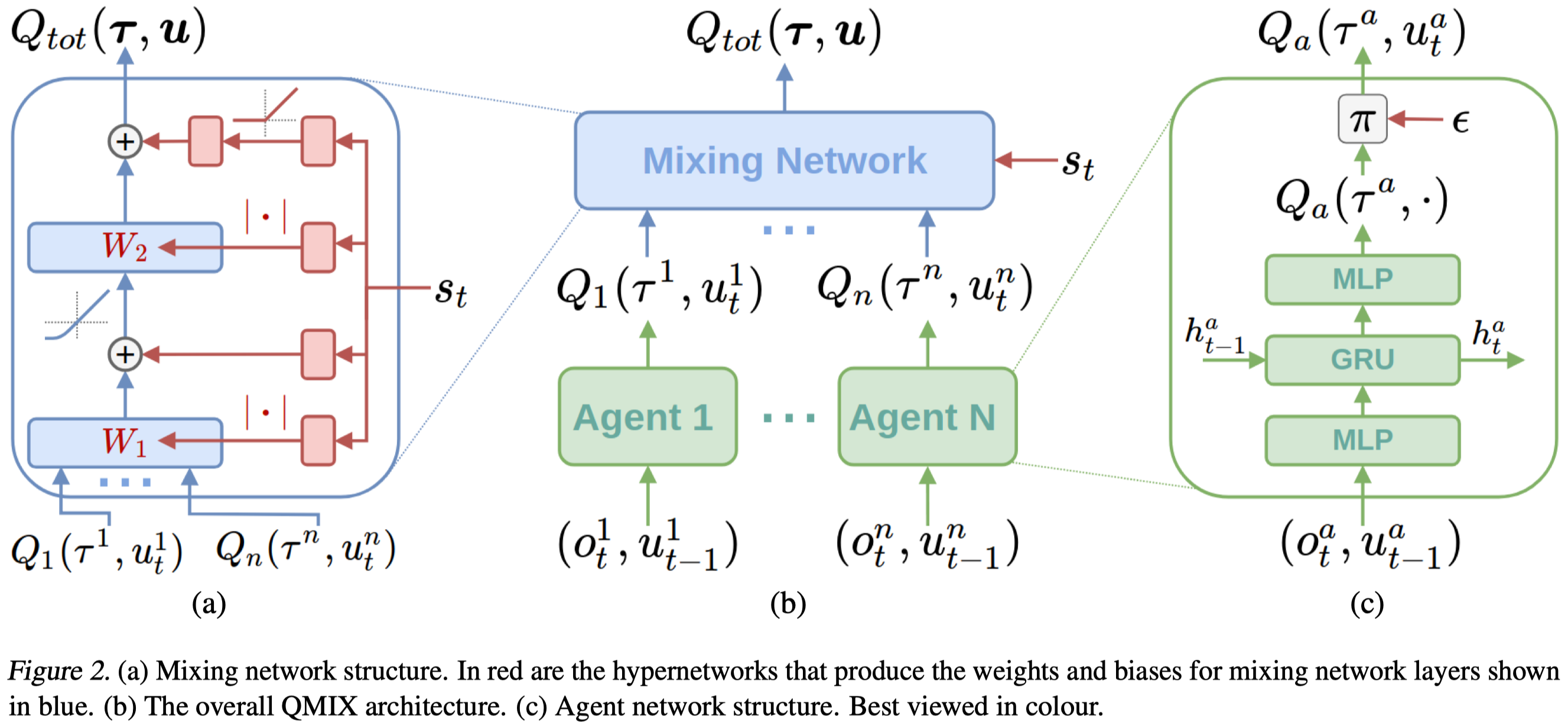
QMIX follows the centralized training and decentralized execution(CTDE) paradigm to allow agents to run separately while training jointly. As a result, QMIX consists of agent networks that represent each \(Q_a\) and a mixing network that combines \(Q_a\)s into \(Q_{tot}\).
As illustrated in Figure2c, the agent network is simply a feed-forward network, optionally including a recurrent unit, that maps the observation and previous action of agent \(a\) to a utility function \(Q_a(\tau^a,\cdot)\). After applying argmax to produce the maximum utility \(Q_a(\tau^a, u_t^a)\), we feed all utilities to a mixing network and compute \(Q_{tot}(\pmb \tau,\pmb u)\). To enforce the monotonicity constraint, all weights in the mixing network should be non-negative. This is achieved by separate hypernetworks, which takes the global state \(s\) as input and generates the weights of each layer in the mixing network. The output of the hypernetwork is a vector, which is shaped into a matrix of appropriate size. Finally, we apply an absolute activation to ensure non-negativity for weights (but not for biases).
Experimental Results

Figure 6 shows that QMIX outperforms both IQN and VDN. VDN’s superior performance over IQL demonstrates the benefits of learning the joint action-value function. QMIX’s superior performance on all maps, especially on maps with heterogeneous agents, demonstrates the benefits of the mixing network.

Figure 7 presents the results fo ablation studies, where QMIX-Lin uses a linear mixing network, QMIX-NS uses a standard network with absolute weights but without the hypernetwork, VDN-S adds a state-dependent term to the sum of the agent’s Q-values(the state-dependent term is produced by a network with a single hidden layer).
From Figure7(a-c), we can see that the state plays the most important role in maps with homogeneous agents. From Figure7(d-f), we learn the importance of the non-linear mixing network produced by the hypernetwork on maps with heterogeneous agents.
Tricks
Several algorithms have been trying to relax the strong assumption made by QMIX. However, Hu et al. 2021 find these methods may not always yield better performance. Instead, they discuss several tricks on QMIX that significantly improve the performance. We distill three of them bellow
- Use Adam instead RMSProp. Adam boosts the network convergence and is more likely to benefit from distributed training.
- Use \(Q(\lambda)\) with a small value of \(\lambda\), where \(Q(\lambda)=(1-\lambda)\sum_{n=1}^\infty \lambda^{n-1}G_n\), in which \(G_n\) is the discounted n-step return. Interestingly, they don’t use Retrace here.
- Small replay buffer. They provide three reasons for this phenomenon: 1) In multi-agent tasks, samples become obsolete faster than in single-agent task. 2) Adam performs better with fast updates. 3) \(Q(\lambda)\) converges more effectively with new samples. I also suspect that it plays an important role that \(Q(\lambda)\) is strongly biased for off-policy data.
References
Rashid, Tabish, Mikayel Samvelyan, Christian Schroeder De Witt, Gregory Farquhar, Jakob Foerster, and Shimon Whiteson. 2018. “QMIX: Monotonic Value Function Factorisation for Deep Multi-Agent Reinforcement Learning.” 35th International Conference on Machine Learning, ICML 2018 10: 6846–59.
Hu, Jian, Haibin Wu, Seth Austin Harding, and Shih-wei Liao. 2021. “Hyperparameter Tricks in Multi-Agent Reinforcement Learning: An Empirical Study.” http://arxiv.org/abs/2102.03479.

