Introduction
We have discussed batch reinforcement learning(BRL) in the previous post, in which we stressed that the poor performance of an offline DDPG agent is caused by the extrapolation error(Fujimoto et al. 2019). In this article, we follow the work of Agarwal et al. 2019, which investigates several advanced algorithms in the BRL setting. Interestingly, Agarwal et al. found that recent advanced off-policy RL algorithms can effectively learn from offline dataset, which may be a sign that the offline DDPG does not work well because of its poor exploitation capacity instead of the extrapolation error.
Off-Policy Algorithms in BRL
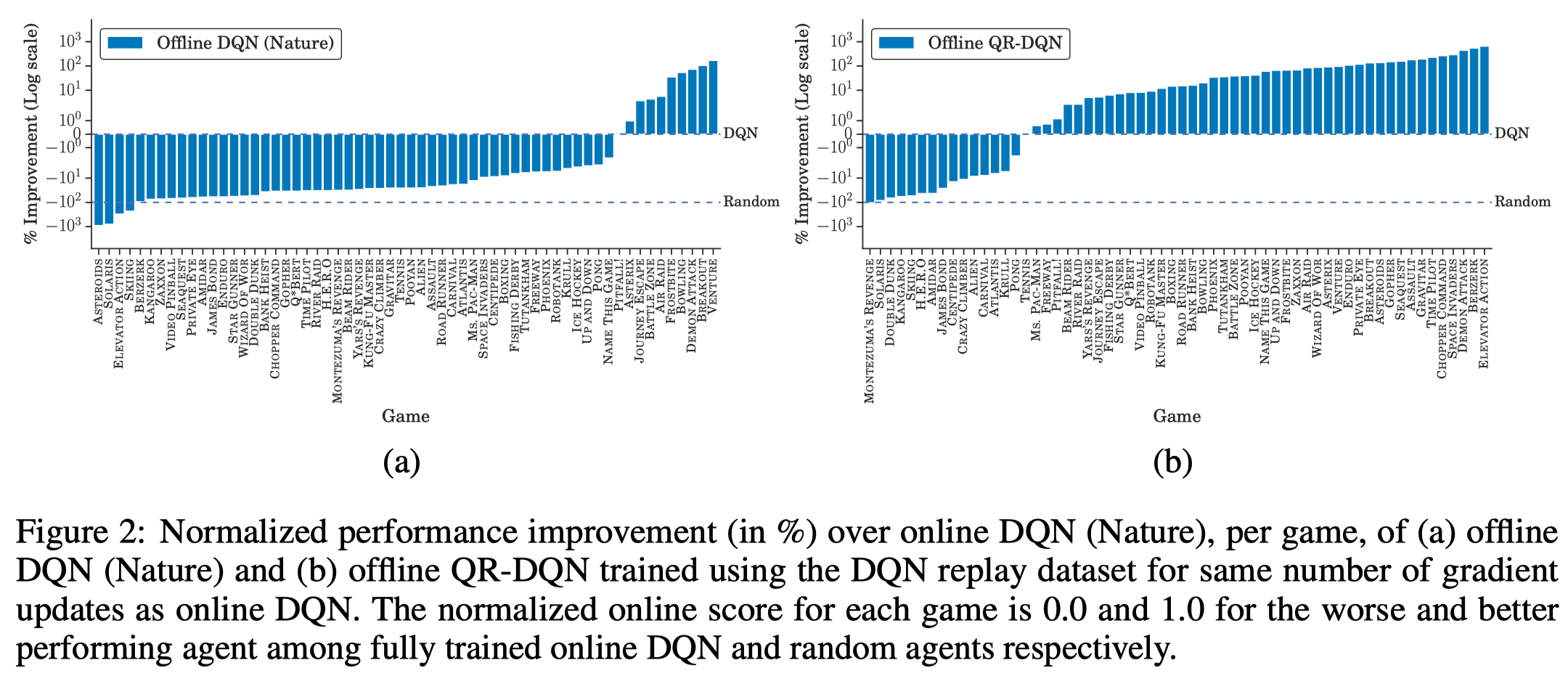
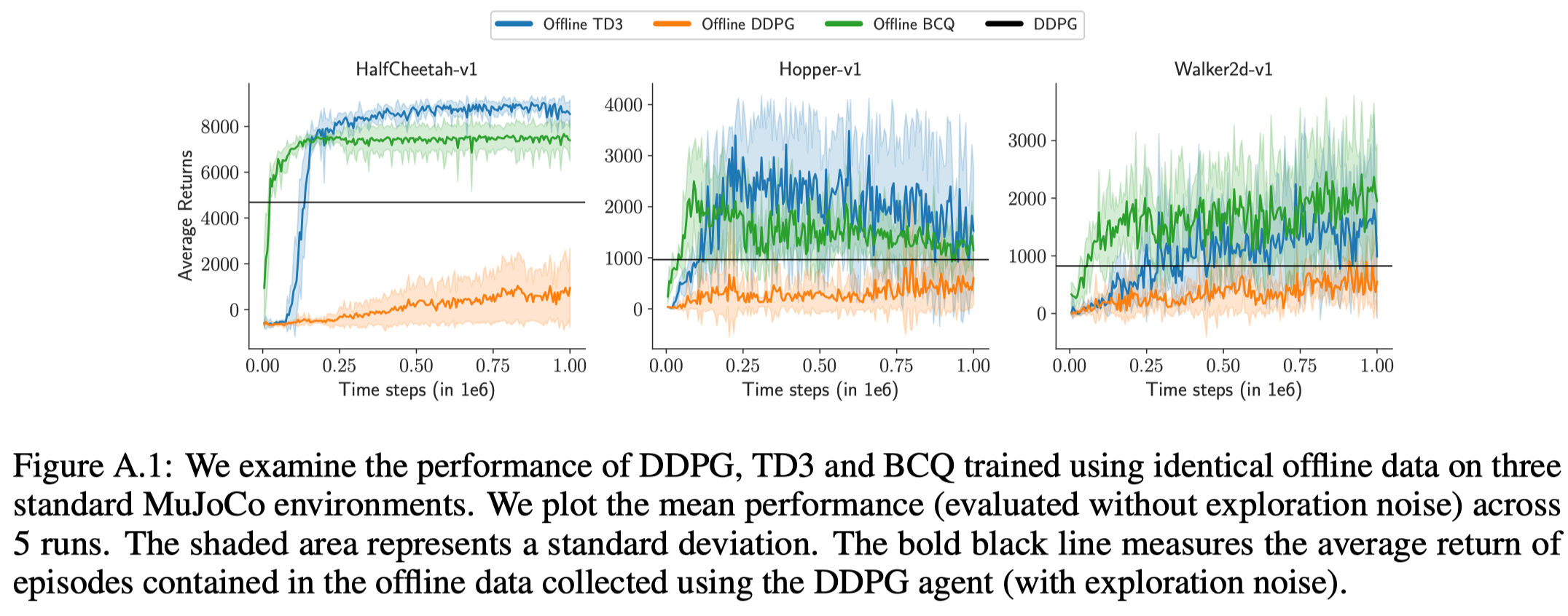
Agarwal et al. investigated several advanced off-policy RL algorithms in BRL setting using final buffer discussed in the previous post. They found that offline QR-DQN significantly outperforms online/offline DQN. The same story also applies to offline TD3 and offline DDPG.
These results also imply that these advanced off-policy RL algorithms is more good at exploitation.
Random Ensemble Mixture
Agarwal et al. propose Random Ensemble Mixture(REM) which combines Emsemble DQN and Dropout. REM maintains a family of \(N\) DQNs(trained with the same hyperparameters). For each step, it randomly samples \(K\) DQNs and applies gradient descent on them. The \(Q\)-value at action-selection step and the target next \(Q\)-value at training step are computed by comparing the sum of \(K\) selected \(Q\)-values:
\[\begin{align} \pi(s)&=\underset{a}{\arg\max}\sum_kQ_k(s,a)\\\ \mathcal L(\theta)&=\mathbb E_{s,a,r,s'\sim\mathcal D}\left[\mathbb E_{\alpha\sim P_{\Delta}}\left[\ell\left(\sum_k\alpha_kQ_k(s,a)-\left(r+\gamma\max_{a'}\sum_{k}\alpha_kQ_k^-(s',a')\right)\right)\right]\right] \end{align}\]where \(\ell\) is the loss function (specifically, the huber loss for DQN) and \(P_\Delta\) represents a probability distribution over the standard \((K-1)\)-simplex \(\Delta^{K-1}={\alpha\in \mathbb R^K:\alpha_1+\alpha_2+\dots+\alpha_K=1,\alpha_k\ge0,k=1,\dots,K}\). In practice, we compute \(\alpha_k\) by first drawing \(\alpha’_k\sim U(0,1)\) and then normalizing them to a categorical distribution \(\alpha_k=\alpha’_k/\sum_i \alpha_i’\).
Experimental Results
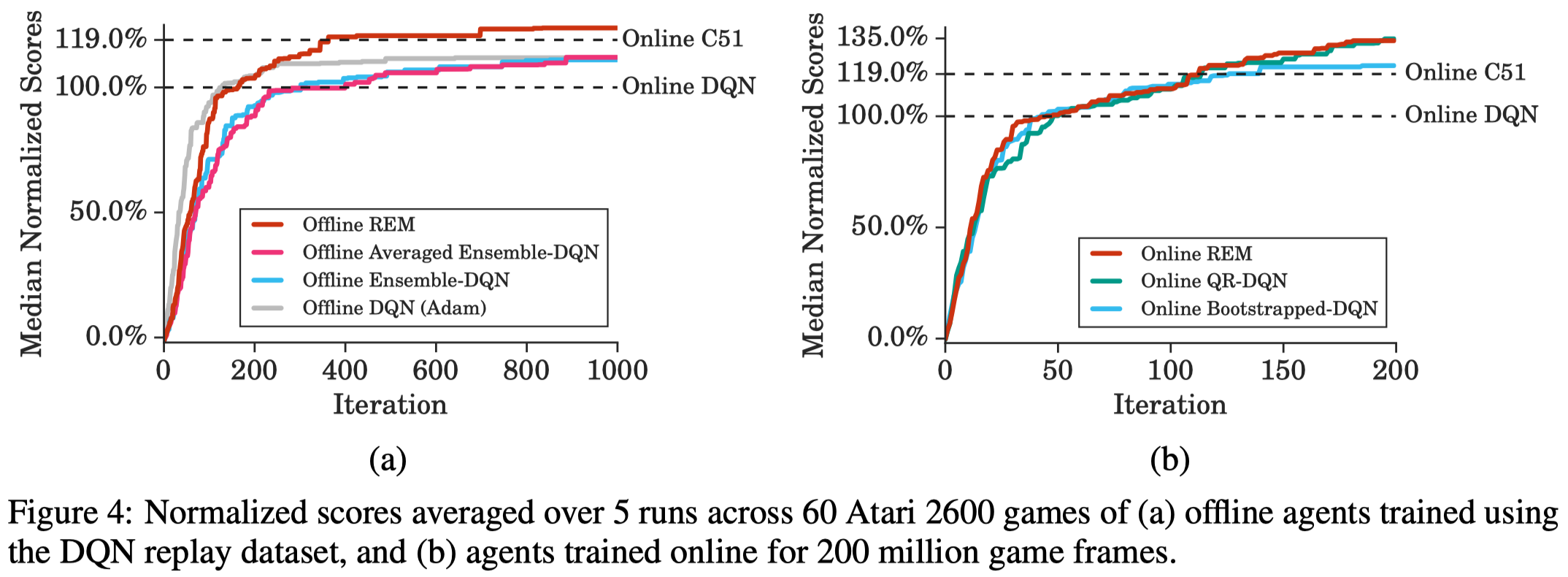
In the online RL, REM samples a \(Q\)-head at the beginning of each episode and run a trajectory accordingly, similar to Bootstrapped DQN. Figure 4.b shows that Online REM achieves performance comparable to QR-DQN without distributional parameterization.
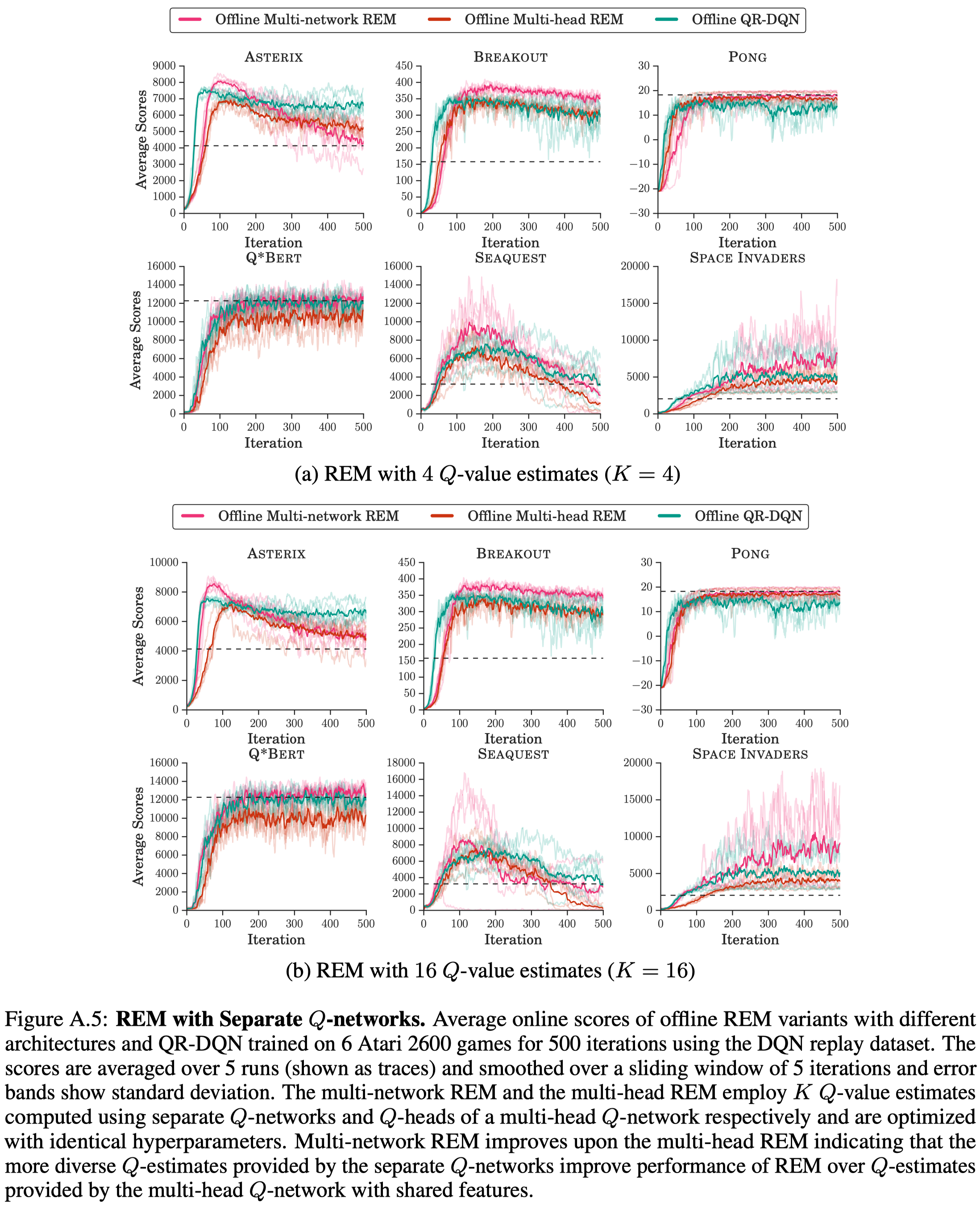
Figure A.5 shows REM with separate \(Q\) networks performs better than REM with multi-head Q network in the offline setting.
References
Rishabh Agarwal, Dale Schuurmans, Mohammad Norouzi. Striving for Simplicity in Off-Policy Deep Reinforcement Learning

