Introduction
PPO is one of the most successful model-free reinforcement learning algorithms and has been successfully applied to solve many challenging tasks, such as DOTA II. Despite its success, its optimization behavior is still ill understood. Wang et al. 2020 investigate the following two questions on PPO:
- If PPO bounds the likelihood ratio \(r(\pi)={\pi(a\vert s)\over\pi_{old}(a\vert s)}\)?
- If PPO enforces a well-defined trust region constraint, i.e., if \(D_{KL}(\pi\Vert\pi_{old})\) is bound?
The answers are quite interesting:
- PPO does not bound the likelihood ratio. The likelihood ratio can grow up to \(4\) in some environments. This is happens due to optimization tricks such as momentum and similar gradients of different samples – e.g., consider two samples with similar gradients. One is out of the clipping range but the other is still in the clip range. Applying gradient descent pushes the out-of-range one further away.
- Answer 1 also implies PPO does not enforce a trust region constraints, such as KL divergence. Furthermore, Wang et al. 2020 shows the KL divergence can be unbounded even when the likelihood ratio is bounded.
From the above Q&As, we can conclude that the main contribution of PPO is clipping gradients from bad samples with large likelihood ratios but not the trust region it’s supposed to impose.
Method
Wang et al. 2020 subsequently propose three methods to enforce the ratio bound and trust-region constraint. As first two can be expressed in the form of general policy loss function, we first express the general loss function as follows
\[\begin{align} \mathcal L(\pi)=\min(r(\pi)A,\mathcal F(r(\pi))A) \end{align}\]where \(r(\pi)\) is the likelihood ratio \(\pi\over{\pi_{old}}\), and \(A\) is the advantage.
We then sequentially discuss each of them and combine them in the end.
PPO with Rollback (PPO-RB)
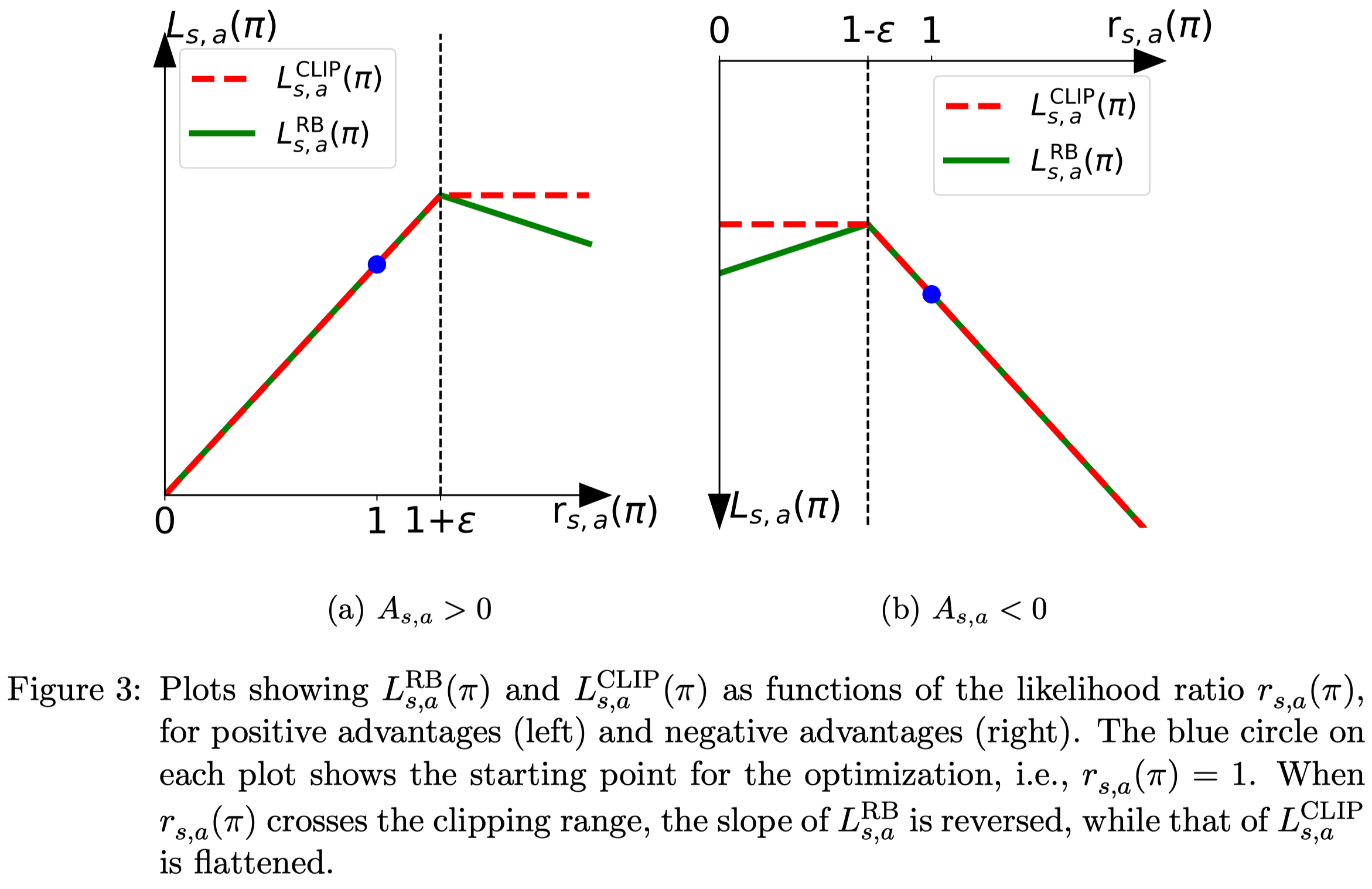
The first method explicitly imposes a penalty on the out-of-range likelihood ratio using a rollback operation
\[\begin{align} \mathcal F^{RB}(r(\pi))= \begin{cases} -\alpha r(\pi)+(1+\alpha)(1-\epsilon)&r(\pi)<1-\epsilon\\\ -\alpha r(\pi)+(1+\alpha)(1+\epsilon)&r(\pi)>1+\epsilon\\\ r(\pi)&\text{otherwise} \end{cases} \end{align}\]where \(\alpha\) decides the force of the rollback and \((1+\alpha)(\cdot)\) here only ensures continuity.
Figure 3 compare \(\mathcal L(\pi)\) with \(\mathcal F^{RB}\) and \(\mathcal F^{CLIP}\), where \(\mathcal F^{CLIP}\) is introduced by the original PPO. The only difference between PPO-RB and PPO is whether to add penalty when the likelihood ratio exceeds the threshold.
Trust Region-based PPO (TR-PPO)
The second method clips the likelihood ratio when the policy \(\pi\) is out of the trust region in terms of the KL divergence:
\[\begin{align} \mathcal F^{RB}(r(\pi))= \begin{cases} 1&D_{KL}(\pi_{old},\pi)\ge \delta\\\ r(\pi)&\text{otherwise} \end{cases} \end{align}\]where \(\delta\) is the threshold. Notice that the KL divergence is computed directly from action distribution rather than from single action point in likelihood ratio. This explicitly clips the objective when the policy is out of the trust region, enforcing the trust region constraint.
Compare to PPO, TR-PPO exames the trust region by the KL divergence instead of the likelihood ratio.
Truly PPO
The last method imposes KL penalty when the new policy diverges away from the old one too much and (possibly erroneously) improve the objectives
\[\begin{align} \mathcal L^{TPPO}=r(\pi)A- \begin{cases} \alpha D_{KL}(\pi_{old},\pi)&D_{KL}(\pi_{old},\pi)\ge \delta\text{ and }r(\pi)A\ge r(\pi_{old})A\\\ \delta& \text{otherwise} \end{cases} \end{align}\]where \(\alpha\) decides the weights of the KL penalty and \(\delta\) is the threshold. \(\delta\) in the otherwise part ensures continuity. By adding the KL penalty, this method mitigates possibly out-of-range improvements caused by similar gradients of different samples and the momentum optimization.
Truly PPO combines both the rollback operation and KL divergence constraint.
Experimental Results
Wang et al. compares PPO and the above three methods on Mujoco and Atari environments. Experiments shows the above methods in deed force more restrictive change to policy update but no obviously performance gain is found. The proposed methods only performs better than PPO in some environments and by a small margin, which is more likely the result of the hyperparameter search.
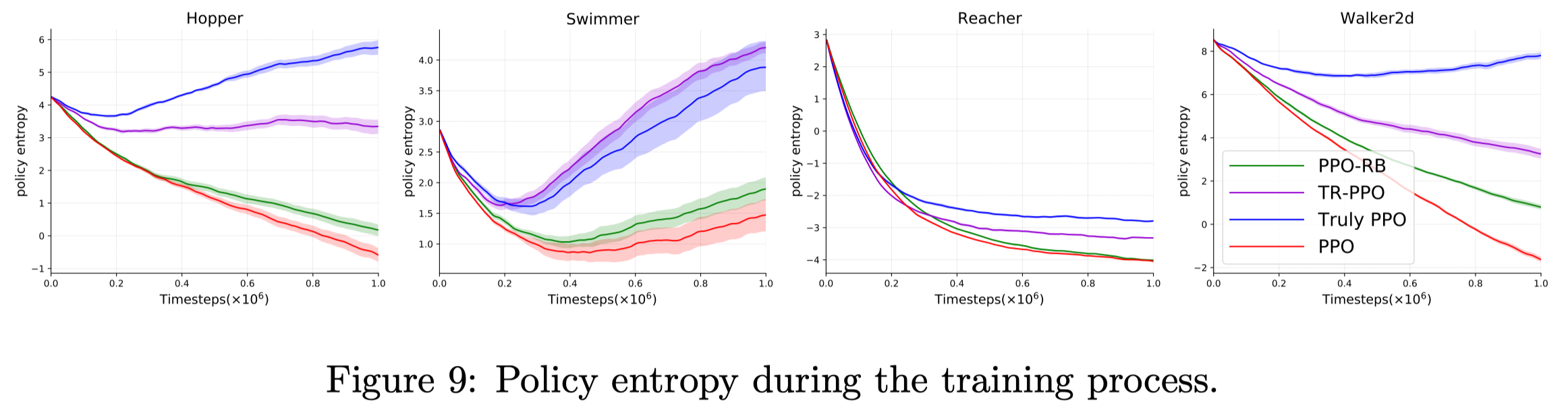
They find the KL divergence constraint usually results in more exploration than the ratio constraint. One explanation is that, in the ratio constraint, the action with larger likelihood updates more often than the others – because \(\pi(a\vert s)\over\pi_{old}(a\vert s)\) is less likely to exceed the bound when \(\pi_{old}(a\vert s)\) is large – making the policy more deterministic and less explore. Figure 9 plots the policy entropy on four Mujoco tasks. We can see that trust region-based methods have higher entropy than ratio-based methods.
References
Wang, Yuhui, and L G Jan. 2020. “Truly Proximal Policy Optimization.”

