Introduction
In this post, we discuss a recurrent architecture built upon LSTM and self-attention that allows us to do relational reasoning in temporal domains. Here, relational reasoning is defined to be the process of understanding the ways in which entities are connected and using this understanding to accomplish some higher order goal. For example, consider sorting the distances of various trees to a park bench: the relations (distances) between the entities (trees and bench) are compared and contrasted to produce the solution, which could not be reached if one reasoned about the properties (positions) of each individual entity in isolation.
Unlike my previous posts, you will see code all over the place in this post since the actual implementation the authors provide is somewhat different from the one they described. All code is originally from [2], modified by myself so that no dependency other than tensorflow is needed.
Multi-Head Dot Product Attention
In the previous post, we have demonstrated that self-attention mechanism leverages dot-product attention to focus on the important part of a sequence and multi-head dot product attention(MHDPA) extends self-attention by introducing multiple head before and after dot-product attention, therefore allowing the model to jointly attent to information from different representation subspaces at different positions. We present the MHDPA in the following figure
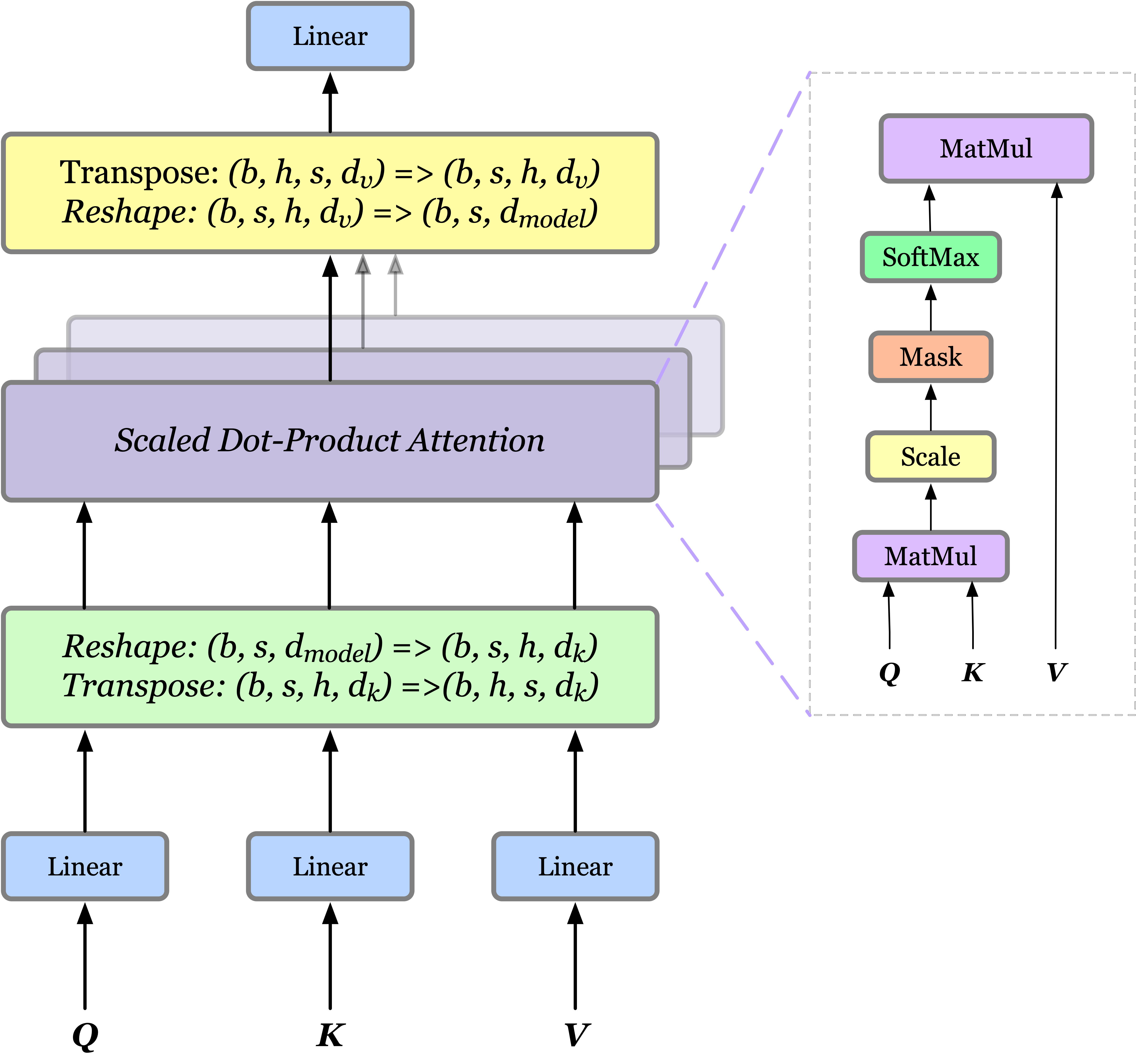
We again mathematically defines MHDPA as
\[\begin{align} \mathrm{MultiHead}(Q,K,V)&=\mathrm{Concat}(\mathrm{head}_1,\dots,\mathrm{head}_h)W^O\tag {1}\\\ where\quad\mathrm{head}_i &=\mathrm{Attention}(QW_i^Q,KW_i^K,VW_i^V)\\\ \mathrm{Attention}(Q,K,V)&=\mathrm{softmax}\left(QK^T\over\sqrt{d_k}\right)V \end{align}\]In general, we use a single matrix of memories \(M\) to represent the queries \(Q\), keys \(K\), and values \(V\) in Eq.\((1)\). One observation is that we could also extend the memories by adding new inputs: we incorporate new inputs into keys and values of the attention, which results in
\[\begin{align} \mathrm{Attention}(MW_i^Q,[M;x]W_i^K,[M;x]W_i^V) \end{align}\]where \([M;x]\) denotes the row-wise concatenation of \(M\) and \(x\). Note that this modification does not change the shape of the output matrix, which makes it possible to work with residual connections and more importantly makes it a valid next memory for recurrent models.
Code
def multihead_attention(memory, key_size, value_size, num_heads):
# Perform linear tranformation to compute all Q, K, V
qkv_size = 2 * key_size + value_size
total_size = qkv_size * num_heads # Denote as F.
qkv = tf.layers.dense(memory, total_size)
qkv = tc.layers.layer_norm(qkv)
mem_slots = memory.get_shape().as_list()[1] # Denoted as N.
# [B, N, F] -> [B, N, H, F/H]
qkv_reshape = tf.reshape(qkv, [-1, mem_slots, num_heads, qkv_size])
# [B, N, H, F/H] -> [B, H, N, F/H]
qkv_transpose = tf.transpose(qkv_reshape, [0, 2, 1, 3])
q, k, v = tf.split(qkv_transpose, [key_size, key_size, value_size], -1)
# softmax(QK^T/(d**2))V
q *= key_size ** -0.5
dot_product = tf.matmul(q, k, transpose_b=True) # [B, H, N, N]
weights = tf.nn.softmax(dot_product)
output = tf.matmul(weights, v) # [B, H, N, V]
# [B, H, N, V] -> [B, N, H, V]
output_transpose = tf.transpose(output, [0, 2, 1, 3])
# [B, N, H, V] -> [B, N, H * V]
new_memory = tf.reshape(output_transpose, [-1, mem_slots, num_heads * value_size])
return new_memory
The actual memory passed in here is the concatenation of the previous memory and input as we will see in RMC function later.
Relational Memory Core
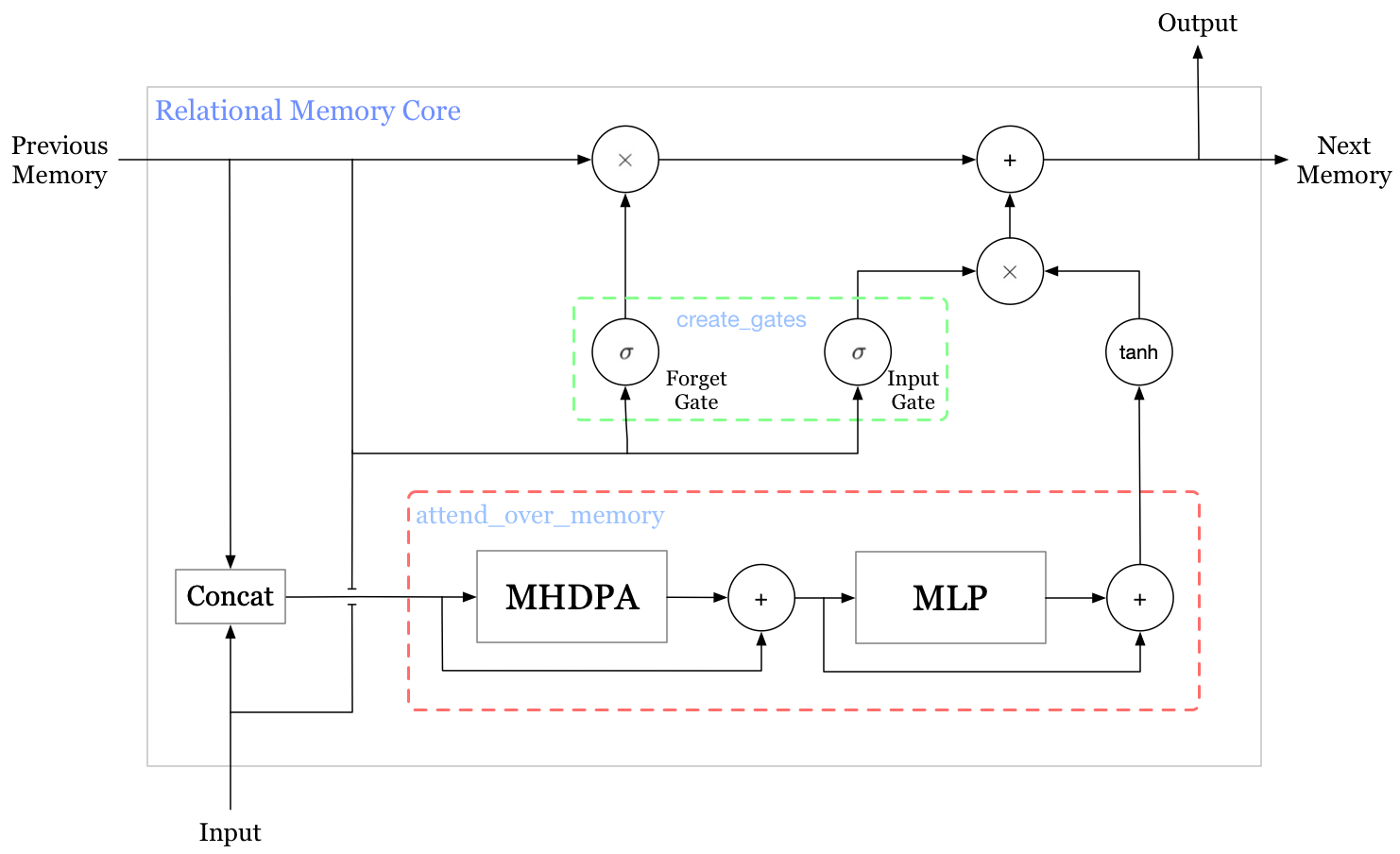
The Relational Memory Core(RMC) is a recurrent core with a matrix of cell states as the above figure illustrates. Note that the RMC depicted above is different from that defined in the paper, but consistent with their provided code — as the authors explained in the paper, they did not found output gates necessary, which makes it resemble GRU. In the rest of this section, we will walk through the code to get a better sense of RMC.
Code
Memory Initialization
def initial_state(batch_size, mem_slots, mem_size):
# [bach_size, mem_slots, mem_size]
init_state = tf.eye(mem_slots, num_columns=mem_size, batch_shape=[batch_size])
return init_state
Different from the general RNN initial state, we uniquely initialize each memory slot to provide variety for the initial state.
Attend over Memory
def attend_over_memory(memory, key_size, value_size, num_heads,
num_mlp_layers, num_blocks=1):
def mlp(x, units_list):
for u in units_list:
x = tf.layers.dense(x, u)
return x
mem_size = num_heads * value_size
for _ in range(num_blocks):
attended_memory = multihead_attention(memory, key_size, value_size, num_heads)
# Add a skip connection to the multiheaded attention's input.
memory = tc.layers.layer_norm(memory + attended_memory)
mlp_memory = mlp(memory, [mem_size] * num_mlp_layers)
# Add a skip connection to the attention_mlp's input.
memory = tc.layers.layer_norm(memory + mlp_memory)
return memory
attend_over_memory in fact has the same architecture as the encoder of the Transformer. It allows each memory attend over all of the other memories and update its content based on the attended information.
Forget & Input Gate
def create_gates(inputs, memory, mem_size, gate_style):
def calculate_gate_size(mem_size, gate_style):
if gate_style == 'unit':
return mem_size
elif gate_style == 'memory':
return 1
else: # gate_style == None
return 0
# We'll create the input and forget gates at once.
# Hence, calculate double the gate size.
num_gates = 2 * calculate_gate_size(mem_size, gate_style)
memory = tf.tanh(memory)
# Do not take the following code as
# split(dense(concat([inputs, memory], 2), num_gates), 2, 2)
# They are different since inputs and memory have different dimension at axis=1
# In this sense, they are more like
# split(dense(concat([inputs + zeros_like(memory), memory], 2), num_gates), 2, 2)
gate_inputs = tf.layers.dense(inputs, num_gates)
gate_memory = tf.layers.dense(memory, num_gates)
gates = tf.split(gate_memory + gate_inputs, num_or_size_splits=2, axis=2)
input_gate, forget_gate = gates
# There is bias terms inside sigmoid in the original implementation,
# which I omit for simplicity here
input_gate = tf.sigmoid(input_gate)
forget_gate = tf.sigmoid(forget_gate)
return input_gate, forget_gate
The input and forget gates serve the same purpose as those in LSTMs, which control how much the old memory to retain and how much new information to let in.
The authors experiment two different kinds of gates: unit gate(the one we use in LSTMs) produces scalars for each individual unit while memory gate produces scalar gates for each memory row.
RMC
def RMC(inputs, memory, key_size, value_size, num_heads,
num_mlp_layers, num_blocks=1, gate_style='unit'):
mem_size = num_heads * value_size
inputs = tf.layers.dense(inputs, mem_size)
if len(inputs.shape.as_list()) == 2:
# reshape inputs so as to be ready to connect to memory
inputs_reshape = tf.expand_dims(inputs, 1)
# Inputs shape: [B, N_i, F]
# Memory shape: [B, N_m, F]
# Memory_plus_input shape: [B, N_m + N_i, F]
memory_plus_input = tf.concat([memory, inputs_reshape], axis=1)
# Next memory shape: [B, N_m + N_i, F]
next_memory = attend_over_memory(memory_plus_input, key_size, value_size, num_heads, num_mlp_layers, num_blocks)
n = inputs_reshape.get_shape().as_list()[1]
# Crop next_memory to restore shape to [B, N_m, F]
next_memory = next_memory[:, :-n, :]
if gate_style == 'unit' or gate_style == 'memory':
input_gate, forget_gate = create_gates(
inputs_reshape, memory, mem_size, gate_style)
next_memory = input_gate * tf.tanh(next_memory)
next_memory += forget_gate * memory
# Output shape: [B, N_m * F]
output = tf.reshape(next_memory, [-1, n * mem_size])
return output, next_memory
Notice that inputs and memory are combined in different ways in attend_over_memory and create_gate: In attend_over_memory, we concatenate memory and inputs along sequential dimension(the second dimension, i.e., dimension \(1\) in code), treating inputs as a memory slot; In create_gate, we actually concatenate memory and inputs along feature dimension(the third dimension, dimension \(2\) in code as the comment suggests), which gives different weights to different features.
Discussion
How does RMC compartmentalize information and learn to compute interactions between compartmentalized information?
RMC compartmentalizes information using a slot-based memory matrix and interact between compartmentalized information with recourse to MHDPA. Furthermore, to introduce temporal relational reasoning, RMC encapsulates these structures in a variant of LSTM cell.
References
- Adam Santoro et al. Relational recurrent neural networks
- Code from DeepMind

