Batch Reinforcement Learning
Batch reinforcement learning(BRL) refers to learning from a fixed dataset \(\mathcal B \) without further interactions with the environment. BRL is hard as there is no cycle where the agent can receive feedback to tell how good or how bad its current policy is.
Extrapolation Error in Batch Reinforcement Learning
Fujimoto et al. argue that batch RL does not work due to extrapolation error in off-policy value learning introduced by the mismatch between the dataset and true state-action visitation of the current policy. They enumerate several factors that contribute to extrapolate error
-
Absent Data: If some state-action pair visited by the current policy do not appear in the dataset, then error is introduced as some function of the amount of similar data and approximation error
- Model Bias: In BRL, the Bellman operator \(\mathcal T^\pi\) is approximated by sampling transition tuples \((s,a,r,s’)\) from the dataset to estimate the transition. However, for a stochastic MDP, without infinite state-action visitation, this could produce a biased estimate of the transition dynamics.
- Training Mismatch: If the distribution of data in the batch does not correspond with the distribution under the current policy, the value function could be a poor estimate of actions selected by the current policy, due to mismatch in training.
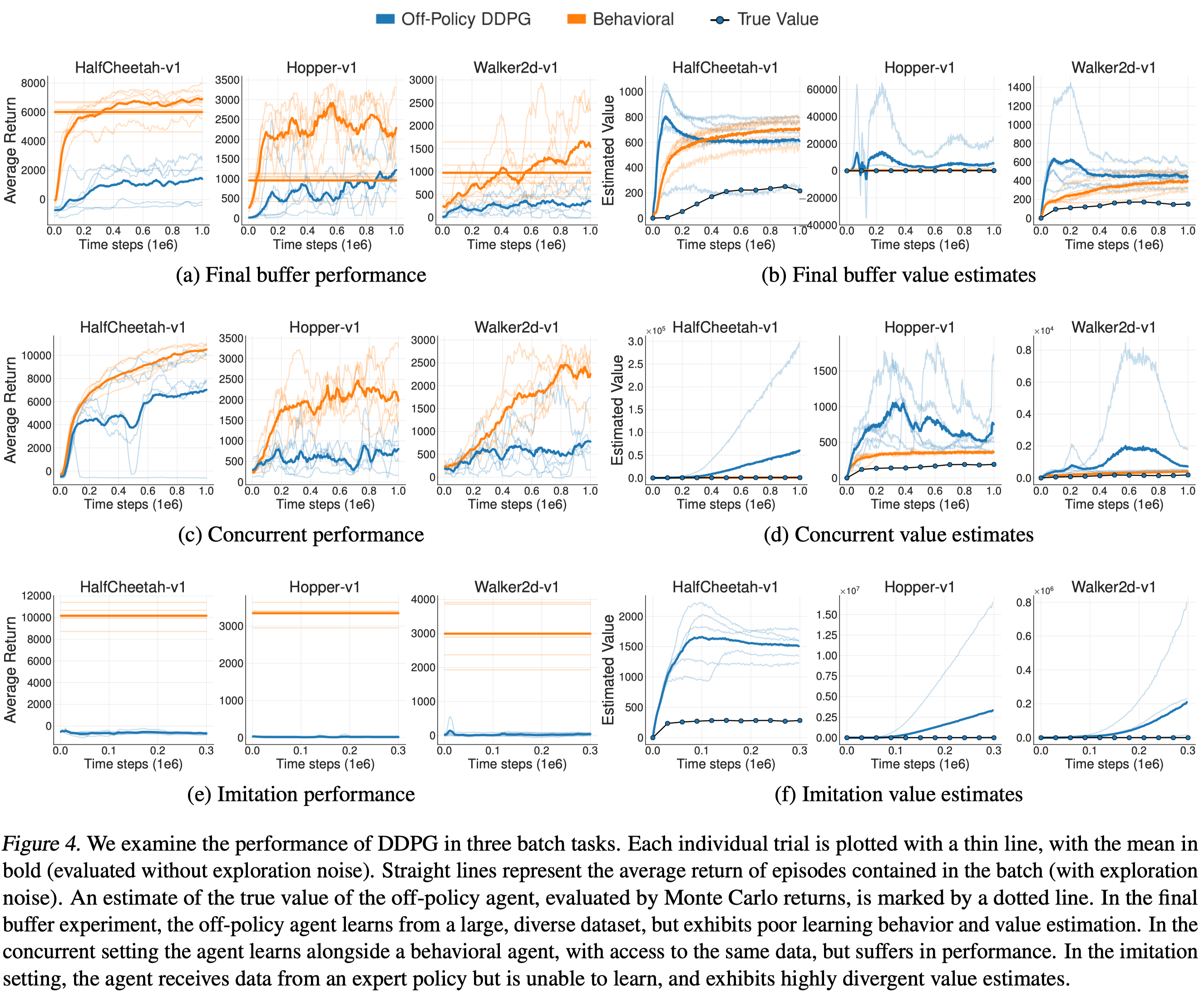
Figure 4 demonstrates the performance and value estimate of DDPG trained in BRL setting compared to those of the behavioral DDPG agent in three different datasets:
- Final Buffer: The off-policy DDPG agent is trained with 1million transitions collected by a DDPG agent(with \(\mathcal N(0, 0.5)\) Gaussian noise to actions) during its training time.
- Concurrent: The off-policy DDPG agent is concurrently trained with the behavior DDPG agent for 1 million time step.
- Imitation: The off-policy DDPG agent is trained with 1 million transitions collected by a trained DDPG agent.
An interesting observation is that, in the imitation dataset, where the off-policy DDPG is trained with data from the expert policy, the agent is unable to learn and the value estimates diverge. This suggests that a traditional RL agent unable to recover the performance of an expert simply using data from the expert policy.
Batch-Constrained Deep Q-Learning
To ameliorate the extrapolation error, Fujimoto et al. propose to restrict the policy so that it induces a similar state-action visitation to the batch, which means to confine the selected actions to the data in the dataset.
Such constrained action is produced using a conditional variational autoencoder(VAE), where the encoder \(E\) maps the state-action pair to a latent variable, and the decoder \(D\) maps the state and latent variable to action. In practice, at each step, they sample \(n\) actions from the conditional VAE and select the highest valued action according to the \(Q\) function as the final action. To increase the diversity of seen actions, they additionally introduce a perturbation model \(\xi_\phi(s,a,\Phi)\), which outputs an adjustment to an action \(a\) in the range \([-\Phi,\Phi]\). This enables access to actions in a constrained region, without having to sample from the generative model a prohibitive number of times. This results in the policy \(\pi\):
\[\begin{align} \pi(s)=\underset{a_i+\xi_\phi(s,a_i,\Phi)}{\arg\max}Q(s,a_i+\xi_\phi(s,a_i,\Phi)),\quad\{a_i\sim D(s, z)\}_{i=1}^n \end{align}\]We train \(\xi_\phi\) and \(Q\) in the same way as TD3. That is, we minimize
Training
The VAE is trained to minimize the regular VAE objective
\[\begin{align} \mathcal L_{VAE} =&(a-\tilde a)^2+D_{KL}(\mathcal N(\mu,\sigma)\Vert\mathcal N(0,1))\\\ &where\quad \tilde a\sim D(s,z),\quad z\sim \mathcal N(\mu, \sigma)\\\ &\qquad\qquad\mu,\sigma= E(s,a),\quad s,a\sim \mathcal B \end{align}\]The perturbation model \(\xi\) is trained to maximize \(Q(s,a)\)
\[\begin{align} \max_\phi Q(s, a+\xi_\phi(s,a,\Phi)), where\ a\sim D(s,z),\ z\sim\mathcal N(0,1) \end{align}\]\(Q\)-networks are optimized towards a twisted double \(Q\)-learning target
\[\begin{align} y=r+\gamma\max_{a_i}\left[\lambda\min_{j=1,2}Q_j(s',a_i)+(1-\lambda)\max_{j=1,2}Q(s',a_i)\right]\tag {13} \end{align}\]They use a convex combination of the two \(Q\) value, with a higher weight \(\lambda=0.75\) on the minimum. The effect of this target is unclear as there is no comparison of it with the target of TD3.
Algorithm 1 summarizes BCQ

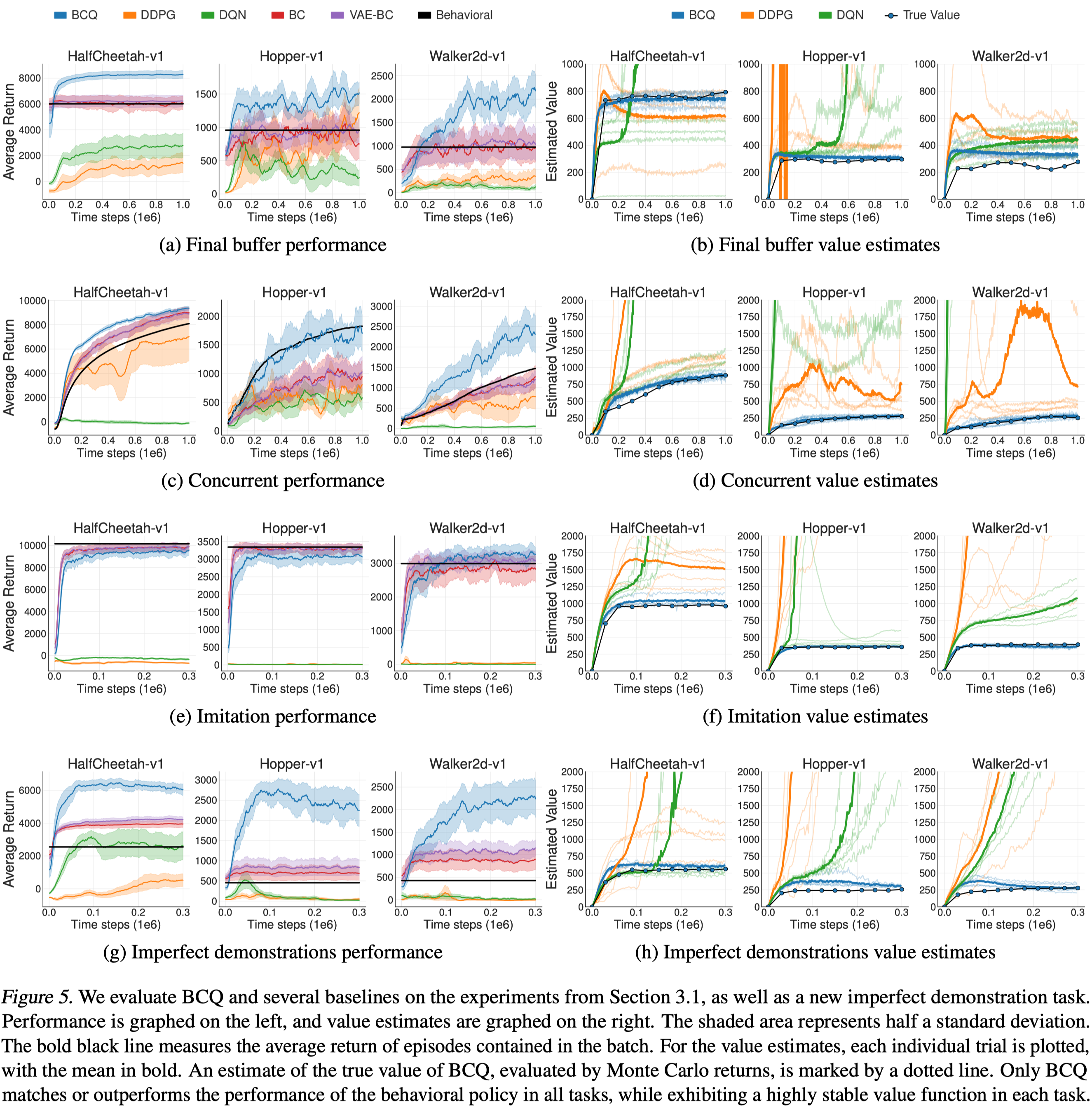
Experimental Results
References
Scott Fujimoto, David Meger, and Doina Precup. Off-policy deep reinforcement learning without exploration

