Introduction
In this post, we will first identify the optimism problem of the probabilistic graphical model discussed in the previous post, then we will address it via variational inference. After that, we will present a dynamic programming algorithm built upon these theoretic results, namely soft value iteration.
The Optimism Problem of The PGM
In the previous post, we mentioned that the \(Q\)-function derived from the backward messages is greater than the \(Q\)-function computed by the Bellman equation. That is,
\[\begin{align}Q_{PGM}(s_t,a_t)&=r(s_t,a_t)+\log \mathbb E_{s_{t+1}\sim p(s_{t+1}|s_t,a_t)}[\exp(V(s_{t+1}))]\\\ &\ge r(s_t,a_t)+\mathbb E_{s_{t+1}\sim p(s_{t+1}|s_t,a_t)}[V(s_{t+1})]=Q(s_t,a_t) \end{align}\]We said that the \(Q\)-function in PGM is optimistic in that it weights more on large \(V(s_{t+1})\). This somewhat changes the transition model, making the transition model conditioned on the optimality sequence, which results in the underlying transition probability biased to the good states, i.e., \(p(s_{t+1}\vert s_t,a_t,O_{1:T}) \ne p(s_{t+1}\vert s_t,a_t)\). It is reasonable to take into account such optimism in our inference problem since in that case optimality is given as evidence, and we can analyze the optimality coming from two sources: we take the right actions or we get lucky. It, however, is not reasonable for control problems because in these problems we do not have information about optimality as a prior and blindly following \(Q_{PGM}\) creates risk-seeking behavior. As a result, Therefore, we should be only concerned about what is the right action to take with respect to the dynamic system, instead of expecting luckiness happens out of nowhere.
Control via Variational Inference
We can address the optimism problem using variational inference. Recall the ELBO
\[\begin{align} \log p(x)&\ge\mathbb E_{z\sim q(z)}\left[\log{p(x,z)\over q(z)}\right]\\\ &=\log p(x)-D_{KL}\left[q(z)\Vert p(z|x)\right] \end{align}\]The second step actually does not make much sense for maximizing \(\log p(x)\) since \(\log p(x)\) appears in both sides, but it gives us a glimpse at what we expect \(q(z)\) to be when we maximize the ELBO w.r.t. \(q(z)\): when we do so, we are trying to align \(q(z)\) with the posterior distribution \(p(z\vert x)\).
Now let us fit our PGM into the variational inference framework. Given the observed variable \(x=O_{1:T}\) and the latent variable \(z=(s_{1:T}, a_{1:T})\), we have
\[\begin{align} \log p(O_{1:T})\ge\mathbb E_{s_{1:T},a_{1:T}\sim q(s_{1:T},a_{1:T})}\left[\log{ p(O_{1:T}, s_{1:T}, a_{1:T})\over q(s_{1:T},a_{1:T})}\right]\tag {1} \end{align}\]Because \(q\) could be any arbitrary distribution, we define it to be the trajectory probability in our control problem:
\[\begin{align} q(s_{1:T},a_{1:T})=p(s_1)\prod_{t=1}^Tp(s_{t+1}|s_t,a_t)q(a_t|s_t)\tag {2} \end{align}\]where \(p(s_1)\) and \(p(s_{t+1}\vert s_t,a_t)\) are known as before, the only thing missing here is the policy \(q(a_t\vert s_t)\). The following figure illustrates both \(p(s_{1:T}, a_{1:T}\vert O_{1:T})\) and \(q(s_{1:T},a_{1:T})\).
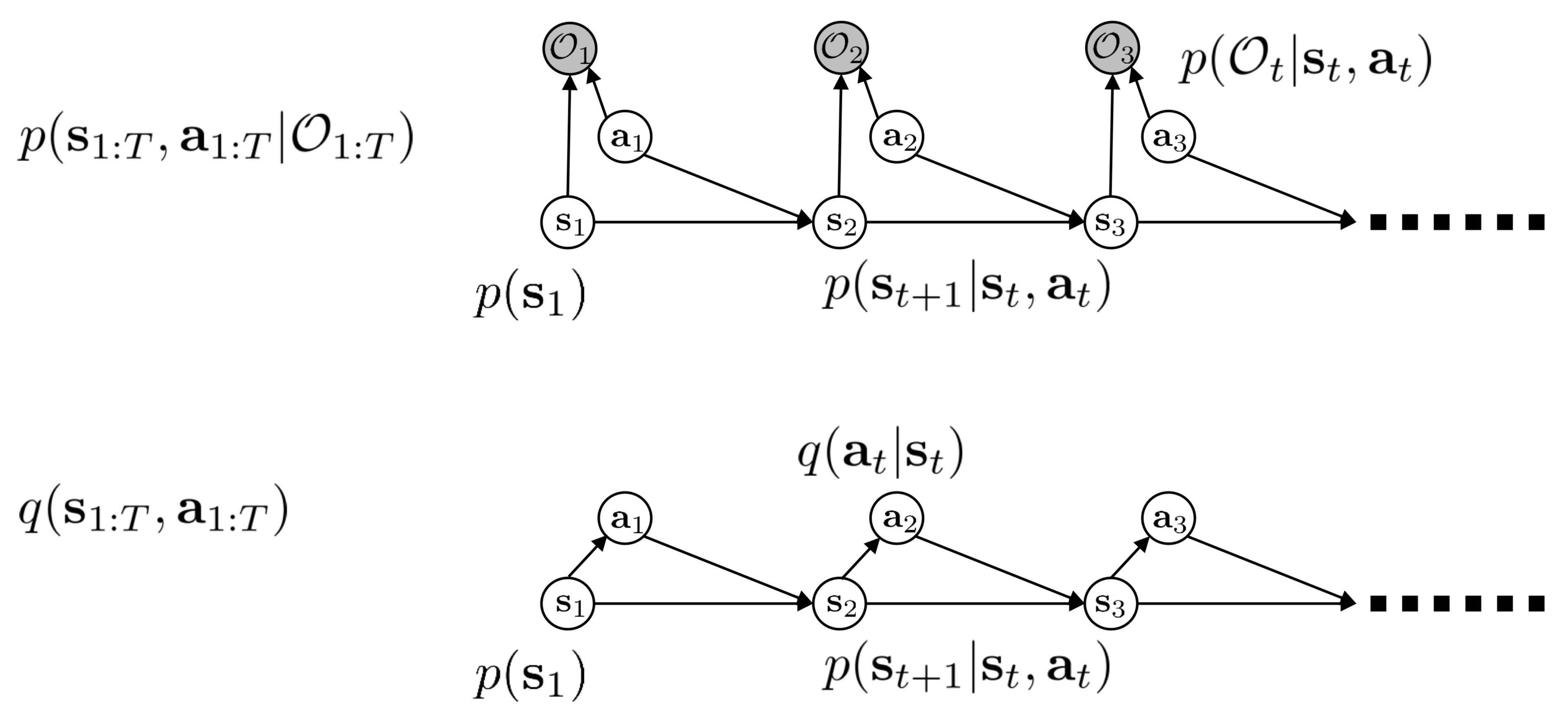
Now we stick Equation \((2)\) back into Equation \((1)\) and have
\[\begin{align} \log p(O_{1:T})\ge&\mathbb E_{s_{1:T}, a_{1:T}\sim q}\left[\log p(s_1) + \sum_{t=1}^T\log p(a_t|s_t)+\sum_{t=1}^T\log p(s_{t+1}|s_t,a_t)+\sum_{t=1}^T\log p(O_t|s_t,a_t)\\\ -\log p(s_1)-\sum_{t=1}^T\log p(s_{t+1}|s_t,a_t)-\sum_{t=1}^T\log q(a_t|s_t)\right]\\\ =&\mathbb E_{s_{1:T}, a_{1:T}\sim q}\left[\sum_{t=1}^T\log p(a_t|s_t)+\sum_{t=1}^T\log p(O_t|s_t,a_t)-\log q(a_t|s_t)\right]\\\ &\qquad\color{red}{p(O_t|s_t,a_t)=k\exp(r(s_t,a_t)),\text{ we ignore the scale factor }k \text{ for now}}\\\ =&\sum_{t=1}^T\mathbb E_{s_{t}, a_{t}\sim q}\left[r(s_t,a_t)-D_{KL}(q(a_t|s_t)\Vert p(a_t|s_t))\right]\tag{3}\\\ &\qquad\color{red}{\text{assume }p(a_t|s_t) \text{ is uniform}}\\\ =&\sum_{t=1}^T\mathbb E_{s_{t}, a_{t}\sim q}\left[r(s_t,a_t)+\mathcal H(q(a_t|s_t))\right]\tag {4} \end{align}\]Note that we ignore the scale factor \(k\) in Eq.\((3)\); we usually instead add a temperature factor to the second term to avoid large-scale reward problem.
Eq.\((4)\) is often referred to as maximum entropy reinforcement learning since it maximizes the policy entropy as well as the conventional policy objective in reinforcement learning. Optimizing it eventually provides us a soft optimal policy. The entropy term is helpful in that it helps to mitigate the model collapse problem, meanwhile, providing some extra bonus for exploration.
Soft Value Iteration Algorithm
Eq.\((3)\) can be directly used as the objective of policy gradient algorithms, but we can also solve it via dynamic programming. Later, we will see that the analysis presented here also sheds some light on how maximum entropy reinforcement leaning cooperates with value functions.
For completeness, we add discount factor \(\gamma\) and temperature \(\alpha\) to Eq.\((3)\). The discount factor discounts future rewards, and the temperature allows us interpolate between the soft max and the hard max: Later we will see in Eq.\((7)\) that as \(\alpha\rightarrow 0\), \(V(s_t)\rightarrow \max(Q(s_t,a_t))\). Now we rewrite the ELBO objective:
\[\begin{align} \mathcal J(q)=\sum_{t=1}^T\gamma^{t-1}\mathbb E_{s_{t}, a_{t}\sim q}\left[r(s_t,a_t)+\alpha\mathcal H(q(a_t|s_t))\right] \end{align}\]As before, we first solve the base case \(q(a_T\vert s_T)\)
\[\begin{align} q(a_T|s_T)=&\underset{q(a_T|s_T)}{\arg\max}\mathbb E_{a_{T}\sim q(a_T|s_T)}[r(s_T,a_T)-\alpha D_{KL}(q(a_T|s_T)\Vert p(a_T|s_T))\\\ =&\underset{q(a_T|s_T)}{\arg\max}\mathbb E_{a_{T}\sim q(a_T|s_T)}\left[\alpha\log\exp \left({1\over\alpha}r(s_T,a_T)\right)-\log{q(a_T|s_T)\over p(a_T|s_T)}\right]\\\ =&\underset{q(a_T|s_T)}{\arg\max}\mathbb E_{a_{T}\sim q(a_T|s_T)}\left[\alpha\log p(a_T|s_T){\exp({1\over\alpha}r(s_T,a_T))\over q(a_T|s_T)}\right]\\\ &\qquad\color{red}{\text{}Z=\int p(a|s_T)\exp\left({1\over\alpha}r(s_T,a)\right)d a}\\\ =&\underset{q(a_T|s_T)}{\arg\max}\alpha\mathbb E_{a_{T}\sim q(a_T|s_T)}\left[\log { { 1\over Z}p(a_T|s_T)\exp({1\over\alpha}r(s_T,a_T))\over q(a_T|s_T)}\right]+\alpha \log Z\\\ =&\underset{q(a_T|s_T)}{\arg\max}-\alpha D_{KL}\left(q(a_T|s_T)\Vert {1\over Z}p(a_T|s_T)\exp\left({1\over\alpha}r(s_T,a_T)\right)\right)+\alpha \log Z\\\ =&{ 1\over Z}p(a_T|s_T)\exp({1\over\alpha}r(s_T,a_T)),\quad\text{the above objective is maximized when KL term is 0}\\\ =&p(a_T|s_T)\exp\left({1\over \alpha}\left(r(s_T,a_T)-\alpha\log Z\right)\right)\\\ =&p(a_T|s_T)\exp\left({1\over\alpha}\Big(Q(s_T,a_T)-V(s_T)\Big)\right)\\\ where\quad &Q(s_T,a_T)=r(s_T,a_T)\\\ &V(s_T)=\alpha\log Z=\alpha\log\int p(a|s_T)\exp\left({1\over\alpha}Q(s_T,a)\right)da \end{align}\]In practice, computing \(V\) using the above equation may cause numerical instability as \(\alpha\) is usually small(around \(1e-3\)) and \({1\over\alpha}Q(s_T,a)\) may blow up to infinity. Noticing that \(V(s_T)\) is also the maximum of the ELBO at state \(s_T\) (or the minimum of the KL divergence between \(q(s_T,a_T)\) and \(p(s_T, a_T\vert O_T)\)), we can compute it as follows
\[\begin{align} V(s_T)=\max_{q(a_T|s_T)}\mathbb E_{a_{T}\sim q(a_T|s_T)}[Q(s_T,a_T)-\alpha D_{KL}(q(a_T|s_T)\Vert p(a_T|s_T))] \end{align}\]Now we compute the recursive case
\[\begin{align} q(a_t|s_t)=\arg\max_{q(a_t|s_t)}\mathbb E_{a_t\sim q(a_t|s_t)} \Big[r(s_t,a_t)-\alpha D_{KL}(q(a_t|s_t)\Vert p(a_t|s_t))+\gamma\mathbb E_{p(s_{t+1}|s_t,a_t)}[V(s_{t+1})]\Big]\tag {4} \end{align}\]Solving it as before, we obtain the optimal policy
\[\begin{align} q(a_t|s_t)=p(a_t|s_t)\exp\left({1\over\alpha}\Big(Q(s_t,a_t)-V(s_t)\Big)\right)\tag {5} \end{align}\]where
\[\begin{align} Q(s_t,a_t)&=r(s_t,a_t)+\gamma\mathbb E_{p(s_{t+1}|s_t,a_t)}[V(s_{t+1})]\tag {6}\\\ V(s_t)&=\alpha\log\int p(a|s_t)\exp\left({1\over\alpha}Q(s_t,a)\right)da \end{align}\]As before, plugging Equation \((5)\) back into Equation \((4)\), we have
\[\begin{align} V(s_t)=\max_{q(a_t|s_t)} \mathbb E_{a_{t}\sim q(a_t|s_t)}[Q(s_t,a_t)-\alpha D_{KL}(q(a_t|s_t)\Vert p(a_t|s_t))]\tag {7} \end{align}\]This give us the soft value iteration algorithm
\[\begin{align} &\mathbf {Soft\ Value\ Iteration\ Algorithm}\\\ &\quad V(s_{T+1})=0\\\ &\quad\mathrm{for}\ t=T\ \mathrm{to}\ 1:\\\ &\quad\quad Q(s_t,a_t)=r(s_t,a_t)+\gamma\mathbb E_{p(s_{t+1}|s_t,a_t)}[V(s_{t+1})]&\forall& s_t,a_t\\\ &\quad\quad V(s_t)=\alpha\log \int p(a_t|s_t)\exp\left({1\over\alpha}Q(s_t,a_t)\right)da_t&\forall& s_t \end{align}\]with policy:
\[\begin{align} \pi(a_t|s_t)=q(a_t|s_t)=p(a_t|s_t)\exp\left({1\over\alpha}\Big(Q(s_t,a_t)-V(s_t)\Big)\right)=p(a_t|s_t)\exp\left({1\over\alpha}A(s_t,a_t)\right) \end{align}\]where \(A\) is different from advantage in our general definition since \(V\) here is soft max over \(Q\) values instead of expectation. Note that this algorithm differs from the one derived from the backward messages only in that it uses the normal Bellman backup when updating action value rather than the optimistic one(it is easy to see when we set both \(\gamma\) and \(\alpha\) to 1).
It is distinct from the regular value iteration in three aspects:
- It is time-based instead of state-based(which indicate it has time complexity \(O(T\times\vert \mathcal S\vert \times \vert \mathcal A\vert )\). It may also be implemented as state-based)
- It uses the soft max instead of the hard max for state value update
- It employs the softmax policy
Recap
In this post, we first addressed the optimism problem of the probabilistic graph model we have discussed in the previous post via variational inference. Then we saw it solved by dynamic programming, obtaining the soft value iteration algorithm. We ended this post with the soft actor-critic algorithm introduced by Haarnoja et al, in which deep neural networks are used.
References
CS 294-112 at UC Berkeley. Deep Reinforcement Learning Lecture 15
Sergey Levine. Reinforcement Learning and Control as Probabilistic Inference: Tutorial and Review
Stuart J. Russeell, Peter Norvig. Artificial Intelligence: A Model Approach

