PEARL — Probabilistic Embedding for Actor-critic RL

Introduction

Meta reinforcement learning could be particularly challenging because the agent has to not only adapt to the new incoming data but also find an efficient way to explore the new environment. Current meta-RL algorithms rely heavily on on-policy experience, which limits their sample efficiency. Most of them also lack mechanisms to reason about task uncertainty when adapting to a new task, limiting their effectiveness in sparse reward problems.

We discuss a meta-RL algorithm that attempts to address these challenges. In a nutshell, the algorithm, namely Probabilistic Embeddings for Actor-critic RL(PEARL) proposed by Rakelly & Zhou et al. in ICLR 2019, is comprised of two parts: It learns a probabilistic latent context that sufficiently describes a task; conditioned on that latent context, an off-policy RL algorithm learns to take actions. In this framework, the probabilistic latent context serves as the belief state of the current task. By conditioning the RL algorithm on the latent context, we expect the RL algorithm to learn to distinguish different tasks. Moreover, this disentangles task inference from action making, which, as we will see later, makes an off-policy algorithm applicable to meta-learning.

The rest of the post is comprised of three parts. First, we introduce the inference architecture, the cornerstone of PEARL. Based on that, we argue the effectiveness of off-policy learning in PEARL and briefly discuss the specific off-policy method adopted by Rakelly & Zhou et al. Finally, we combine both these components to form the final algorithm PEARL.

Inference Architecture

Inference network captures knowledge about how the current task should be performed in a latent probabilistic context variable $Z$, on which we condition the policy as $\pi_\theta(a\vert s,z)$ in order to adapt its behavior to the task. In this section, we focus on how the inference network leverages data from a variety of training tasks to learn to infer the value of $Z$ from a recent history of experience in the new task.

For a specific task, we sample a batch of recently collected transitions and encode each transition $c_n$ through an inference network $\phi$ to distill the probabilistic latent context $\Psi_\phi(z\vert c_n)$, a Gaussian posterior. Then we compute the product of all these Gaussian factors to form the posterior over the latent context variables:

\[\begin{align} q_\phi(z|c)=\prod_{n=1}^N\Psi_\phi(z|c_n) \end{align}\]

A potential advantage of this simple product is that it introduces permutation invariant representation $q_\phi(z\vert c)$.

The following figure demonstrates this process

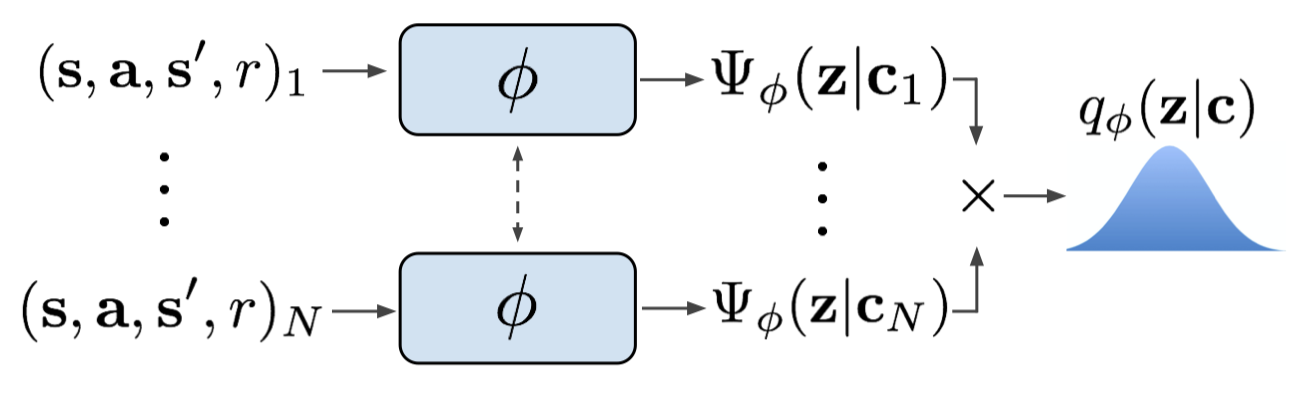
Notice that transitions used here are randomly sampled from a set of recently collected transitions, which differs from transitions we later use to train the off-policy algorithm. The authors also experiment with other architectures and sampling strategies, such as RNN with sequential transitions, none of them exhibit superior performance.

Inference Network Optimization

We optimize the inference network $q_\phi(z\vert c)$ through the variational lower bound:

\[\begin{align} \mathbb E_{z\sim q_\phi(z|c)}\left[R(\mathcal T,z)+\beta D_{KL}(q_\phi(z|c)\Vert \mathcal N(0, I))\right] \end{align}\]

where $R$ is the objective of some downstream task, and $\mathcal N(0,I)$ is a unit Gaussian prior. One could easily derive this objective follows the derivation of $\beta$-variational autoencoder if we take $R$ as the reconstruction loss. The authors found empirically that training the encoder to recover the state-action value function(with $Q$-function) outperforms optimizing it to maximize actor returns(with policy), or to reconstruct states and rewards(with a VAE structure).

Why Not Use Deterministic Context?

The advantage of a probabilistic context is that it can model the belief state of the task, which is crucial for the downstream off-policy algorithm to achieve deep exploration. Deep exploration is particularly important in sparse reward setting in which a consistent exploration strategy is more efficient than random exploration. We refer the interested reader to Section 5 of Osband et al. 2016 for an illustrative example. The following figure compares these two contexts on a 2D navigation problem with sparse reward.

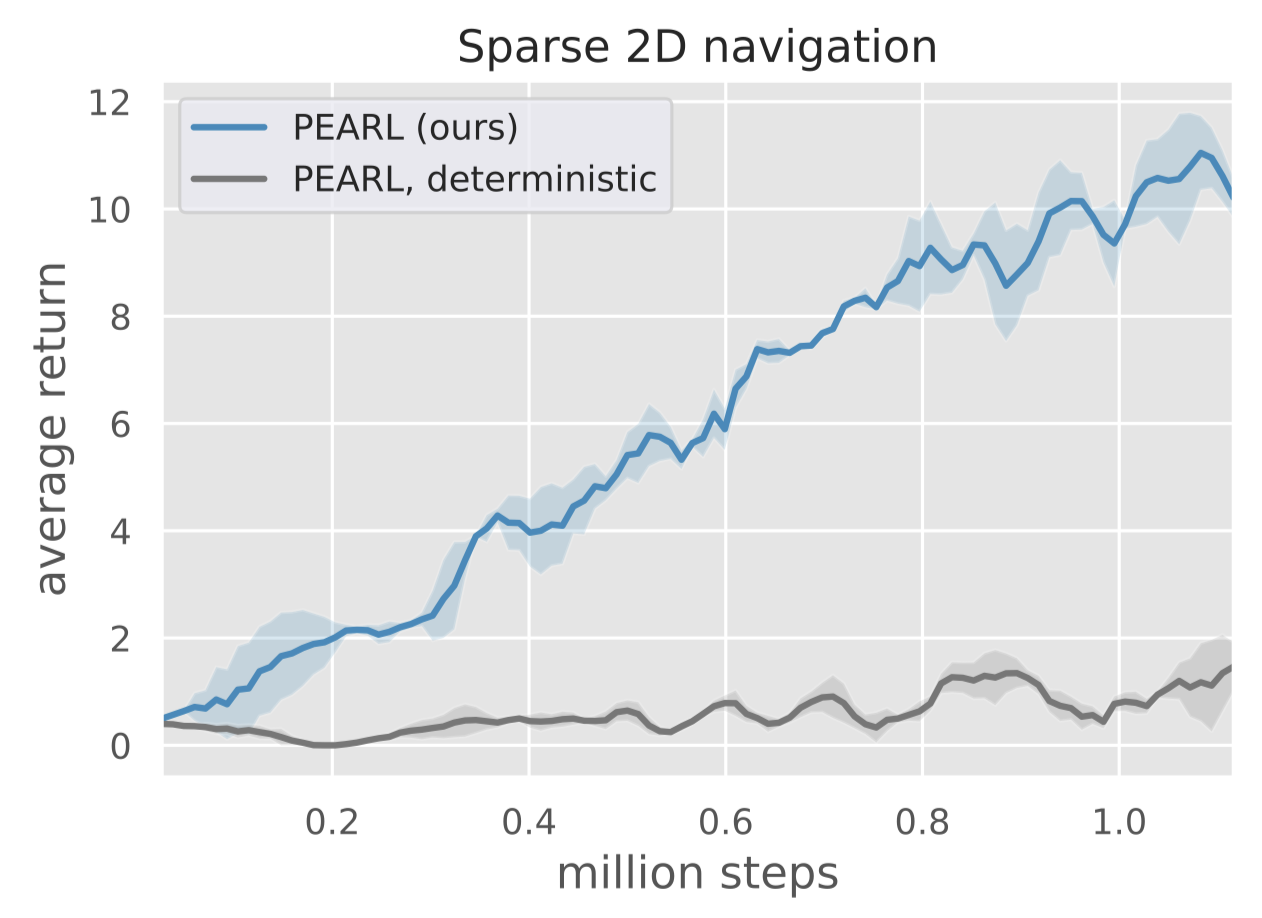
Performance comparison between deterministic and stochastic context

Combine Off-Policy RL with Meta-Learning

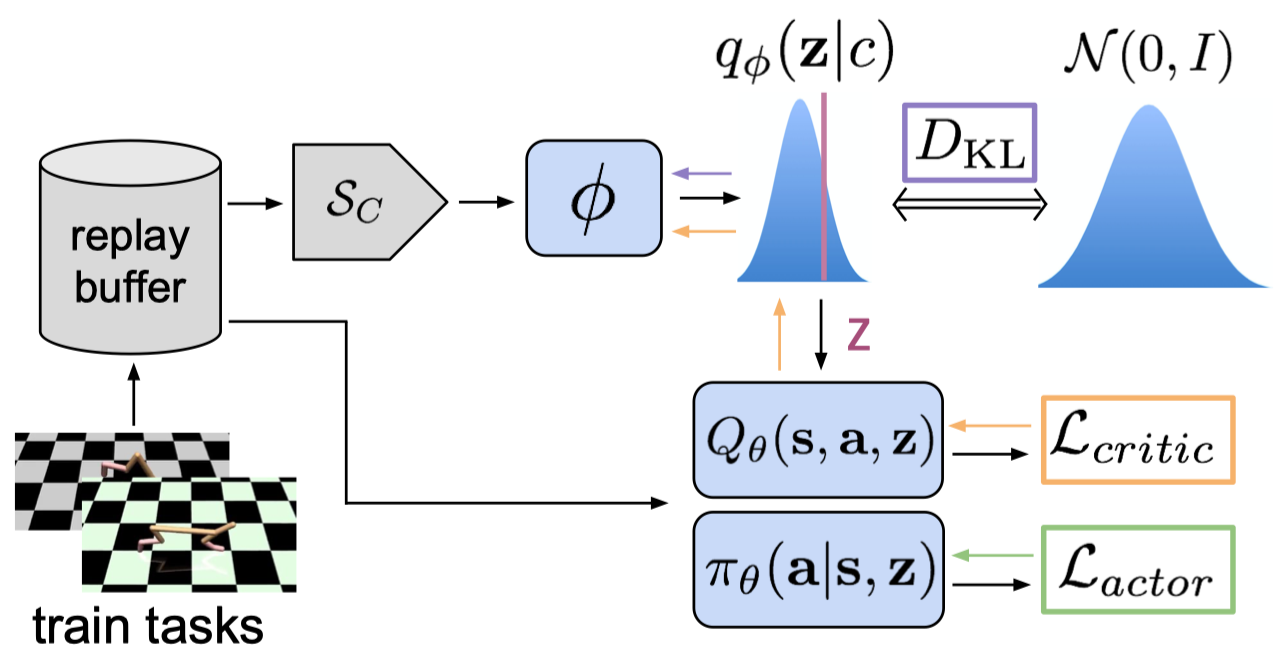
Modern meta-learning algorithms primarily rely on the assumption that the distribution of data used for adaptation will match across meta-training and meta-test. In RL, this implies that on-policy data should be used during meta-training since at meta-test time on-policy data will be used for adaptation. PEARL frees this constraint by offloading the burden of task inference from the RL method onto the inference network. Doing so, PEARL no longer need to fine-tune the RL method at meta-test time and can apply off-policy learning at meta-training. In fact, the only modification to an off-policy RL method here is to condition each network on $z$ and leave others as they are.

The official implementation of PEARL adopts Soft Actor-Critic(SAC) since SAC exhibits good sample efficiency and stability, and further has a probabilistic interpretation which integrates well with probabilistic latent contexts. Long story short, SAC consists of five networks: two state-value functions $V$ and $\bar V$($\bar V$ is the target network of $V$), two action-value functions $Q_1$ and $Q_2$, and a policy function $\pi$; it optimizes these functions through the following objectives

\[\begin{align} \mathcal L_Q&=\mathbb E_{s_t,a_t, s_{t+1}\sim \mathcal B,z\sim q(z|c)}\left[\big(r(s_t,a_t)+\gamma \bar V(s_{t+1}, \bar z)-Q_i(s_t,a_t, z)\big)^2\right]\quad \mathrm{for}\ i\in\{1,2\}\\\ \mathcal L_V&=\mathbb E_{s_t,a_t\sim \mathcal B,z\sim q(z|c)}\left[\big(Q(s_t,a_t, z)-\alpha\log \pi(a_t|s_t, \bar z)-V(s_t, \bar z)\big)^2\right]\\\ \mathcal L_\pi&=\mathbb E_{s_t\sim \mathcal B, z\sim q(z|c), a_t\sim\pi(a_t|s_t,z)}\left[\alpha\log \pi(a_t|s_t, \bar z)-Q(s_t,a_t,z_t)\right] \end{align}\]

where $Q=\min(Q_1,Q_2)$ and $\bar z$ indicates that gradients are not being computed through it.

Algorithm

Meta-Training

\[\begin{align} &\mathbf{Algorithm}\ \mathrm{meta\_training}(\mathrm{Batch\ of\ training\ tasks\ }\{\mathcal T_i\}\mathrm{\ from\ p(\mathcal T)}):\\\ 1.&\quad\mathrm{initialize\ RL\ replay\ buffers\ }\mathcal B^i\mathrm{\ for\ each\ training\ task}\\\ 2.&\quad \mathbf{while}\ not\ done\ \mathbf{do}\\\ 3.&\quad\quad\mathbf{for}\ each\ \mathcal T_i\ \mathbf{do}\quad \#\ sampling\ data\\\ 4.&\quad\quad\quad\mathrm{initialize\ context\ buffer\ }\mathcal C^i=\{\}\\\ 5.&\quad\quad\quad\mathbf{for}\ each\ task\ \mathcal T_i\ \mathbf{do}\\\ 6.&\quad\quad\quad\quad\mathrm{sample\ }z\sim\mathcal N(0,I)\quad\#\ prior\ distribution\\\ 7.&\quad\quad\quad\quad\mathrm{collect\ data\ by\ running\ }\pi_{\theta}(a|s,z)\ \mathrm{on\ task}\ \mathcal T_i\ \mathrm{and\ add\ data\ to\ }\mathcal C^i\ \mathrm{and}\ \mathcal B^i\\\ 8.&\quad\quad\quad\quad\mathrm{sample\ }z\sim q_\phi(z|c)\quad \#\ posterior\ distribution\\\ 9.&\quad\quad\quad\quad\mathrm{collect\ data\ by\ running\ }\pi_{\theta}(a|s,z)\ \mathrm{on\ task}\ \mathcal T_i\ \mathrm{and\ add\ data\ to\ }(\mathcal C^i\ \mathrm{and})\ \mathcal B^i\\\ 10.&\quad\quad\mathbf{for}\ each\ step\ in\ training\ steps\ \mathbf{do}\quad \#\ training\\\ 11.&\quad\quad\quad\mathbf{for}\ each\ \mathcal T_i\ \mathbf{do}\\\ 12.&\quad\quad\quad\quad\mathrm{sample\ context\ }c\sim \mathcal C^i\mathrm{\ and\ RL\ batch}\ b^i\sim\mathcal B^i\\\ 13.&\quad\quad\quad\quad\mathrm{sample\ }z\sim q_\phi(z|c)\\\ 14.&\quad\quad\quad\quad\mathrm{update\ inference\ network\ jointly\ with\ SAC\ using\ }b^i \end{align}\]

There are several things worth attention:

The context $c$ is usually a tuple $(s, a, r)$; it may also include $s’$ for task distributions in which the dynamics change across tasks.
There is an implicit for-loop wrapping Lines 6&7 such that $z$ is resampled after each trajectory. The same story goes with Lines 8&9. Also, notice that in many tasks we do not add data collected at Line 9 to the context buffer(num_steps_posterior is zero in most configurations); This suggests that the context $c$ in line 12 are collected by policy conditioned on $z$ from the prior distribution. Rakelly&Zhou et al. found this setting worked better for these shaped reward environments, in which exploration does not seem to be crucial for identifying and solving the task.[5]
The inference network $q_\phi(z\vert c)$ is trained using gradients from the Bellman update of the $Q$-network as we stated before.

Meta-Test

\[\begin{align} &\mathbf{Algorithm}\ \mathrm{meta\_test}(\mathcal T \sim p(\mathcal T)):\\\ 1.&\quad\mathrm{initialize\ context\ }c=\{\}\\\ 2.&\quad\mathbf {for}\ k=1,\dots, K\ \mathbf{do}\\\ 3.&\quad\quad\ \mathrm{sample}\ z\sim q_\phi(z|c)\\\ 4.&\quad\quad\ \mathrm{run\ a\ trajectory\ using\ policy\ }\pi(a|s,z)\ \mathrm{and\ add\ data\ to\ }c \end{align}\]

Unlike previous methods, PEARL does not fine-tune any network at meta-test; it relies on the generalizability of the inference network to adapt new tasks.

Experimental Results

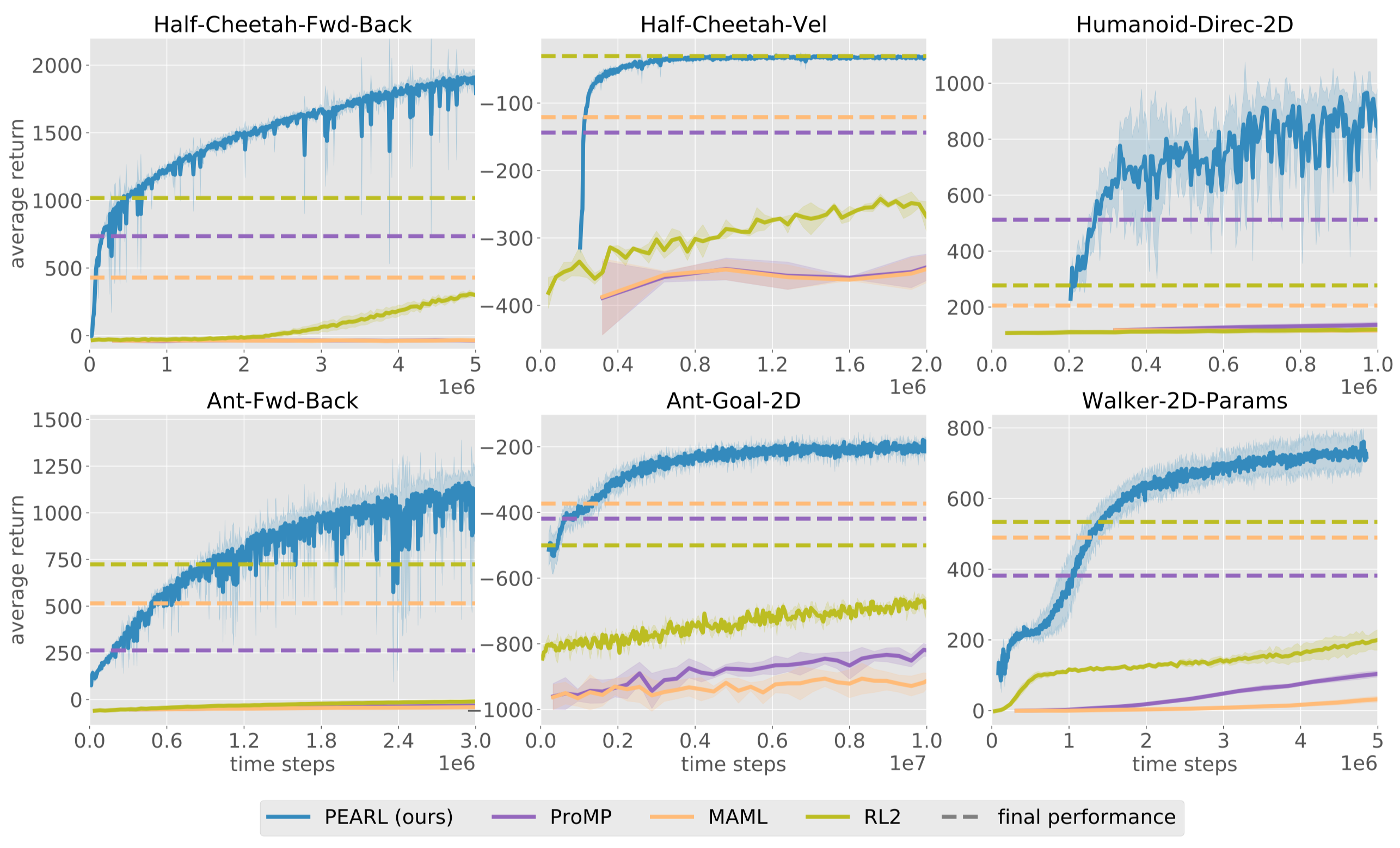
The above figure demonstrates the task performance of different approaches on six continuous control environments. These locomotion task families require adaptation across reward functions (walking direction for Half-CheetahFwd-Back, Ant-Fwd-Back, Humanoid-Direc-2D, target velocity for Half-Cheetah-Vel, and goal location for Ant-Goal2D) or across dynamics (random system parameters for Walker-2D-Params). RL$^2$ is implemented with PPO, MAML is implemented with TRPO.

Discussion

PEARL relies on the generalization of the inference network to adapt new tasks. In the training time, the task uncertainty is deminished as the inference network learns from the task data. This anneals exploration via posterior sampling and improves the task performance gradually. However, this is not true at meta-test time when we do not perform any optimization. Maybe we can as well optimize the inference network to improve the performance of task inference.

Reference

Kate Rakelly, Aurick Zhou, Deirdre Quillen, Chelsea Finn, and Sergey Levine. Efﬁcient Off-Policy Meta-Reinforcement Learning via Probabilistic Context Variables
Ian Osband, Charles Blundell, Alexander Pritzel, and Benjamin Van Roy. Deep Exploration via Bootstrapped DQN
Tuomas Haarnoja, Aurick Zhou, Pieter Abbeel, and Sergey Levine. Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor
code: https://github.com/katerakelly/oyster
https://github.com/katerakelly/oyster/issues/8#issuecomment-525923243